Question

【题目】已知点是直线上一点，，是的平分线．

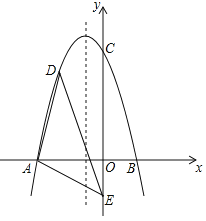
（1）当点，在直线的同侧，且在的内部时（如图1所示 ）， 设，求的大小；

（2）当点与点在直线的两旁（如图2所示），（1）中的结论是否仍然成立？请给出你的结论，并说明理由；

（3）将图2 中的射线绕点顺时针旋转，得到射线，设，若，则的度数是 （用含的式子表示）

Answer 1

【答案】（1） ；（2）（1）中的结论不变，即，理由见解析；（3） ．

【解析】

（1）设，表达出∠BOE，∠COF的大小，再根据列出方程求解即可；

（2）类比（1）的求法，表达出∠BOE，∠COF，列出方程求解即可；

（3）对于旋转后OD的位置分两种情况讨论，通过角的运算，表达出∠DOE的度数，再根据题意，排除射线OD在∠BOE外部的情况．

解：（1）设，则

，即

（2）（1）中的结论不变，即

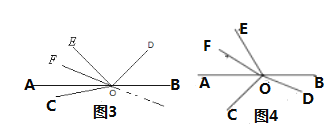
（3）

分为两种情况：

①如图3，射线在的内部，则

∠DOE=180°-∠BOD-∠AOE

②如图4，射线在的外部，则

此时

∵∠AOC<∠COE

即n<60°，

∴，

又∵

∴射线不可能在的外部

综上所述：的度数为．