题目内容
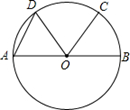
如图,△ABC是⊙O的内接三角形,点C是优弧AB上一个动点(不与A、B重合)。设∠OAB=α,∠C=β
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明。

(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明。

解:(1)连接OB,则∠OBA=∠OAB=35° ∴∠AOB=110°∴∠C= 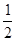 ∠AOB=55°
∠AOB=55°
(2)α+β=90°
β=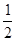 ∠AOB=
∠AOB=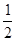 (180°-2α)=90°-α
(180°-2α)=90°-α
即α+β=90°
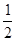 ∠AOB=55°
∠AOB=55°(2)α+β=90°
β=
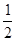 ∠AOB=
∠AOB=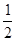 (180°-2α)=90°-α
(180°-2α)=90°-α即α+β=90°
(1)同弧所对的圆心角等于圆周角的二倍;
(2)三角形内角和为180度,利用角的关系可知α+β=90°。
(2)三角形内角和为180度,利用角的关系可知α+β=90°。

练习册系列答案
相关题目
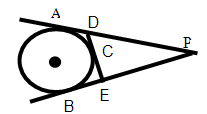

 B
B C8 D
C8 D
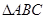 中,AB=" 4" cm,BC="2" cm,
中,AB=" 4" cm,BC="2" cm,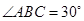 ,把
,把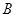 为中心按逆时针方向旋转,使点
为中心按逆时针方向旋转,使点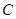 旋转到
旋转到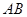 边的延长线上的点
边的延长线上的点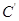 处,那么
处,那么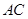 边扫过的图形(图中阴影部分)的面积是____________ cm2.
边扫过的图形(图中阴影部分)的面积是____________ cm2. 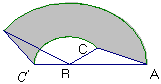
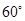 的圆心角所对的弦长为 .
的圆心角所对的弦长为 . 是⊙
是⊙ 的直径,弦
的直径,弦 ,垂足为
,垂足为 ,如果
,如果 ,
, ,那么线段
,那么线段 的长是 .
的长是 .