题目内容
如图所示，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是
- A.12cm
- B.10cm
- C.14cm
- D.无法确定
B
分析：根据两点之间，线段最短．先将图形展开，再根据勾股定理可知．
解答：如图所示：
可以把A和B展开到一个平面内，
即圆柱的半个侧面是矩形：
矩形的长BC=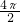
=2π=6，矩形的宽AC=8，
在直角三角形ABC中，AC=8，BC=6，
根据勾股定理得：AB=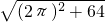
≈10．
故选B．
点评：要求不在同一个平面内的两点之间的最短距离，需要把两个点展开到一个平面内，再计算．
分析：根据两点之间，线段最短．先将图形展开，再根据勾股定理可知．
解答：如图所示：
可以把A和B展开到一个平面内，
即圆柱的半个侧面是矩形：
矩形的长BC=
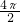=2π=6，矩形的宽AC=8，在直角三角形ABC中，AC=8，BC=6，
根据勾股定理得：AB=
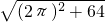≈10．故选B．
点评：要求不在同一个平面内的两点之间的最短距离，需要把两个点展开到一个平面内，再计算．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
4、
如图所示，一圆柱高8cm，底面半径为2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是（ ）
如图所示，一圆柱高8cm，底面圆周长为12cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路线是（ ）cm．