Question

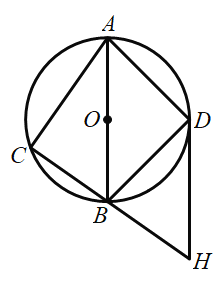
【题目】在平面直角坐标系中，矩形ABCD的边BC在轴上，顶点，连接AC按照下列方法作图：（1）以点C为圆心，适当的长度为半径画弧分别交CA,CD于点E，F；（2）分别以点E，F为圆心，大于的长为半径画弧交于点G；（3）作射线CG交AD于H，则点H的横坐标为（ ）

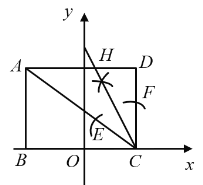
A.6B.4C.3D.1

Answer 1

【答案】D

【解析】

根据可得AB=6，BC=8，由勾股定理得AC=10，过H作HQ⊥AC，由角平分线的性质得HQ=HD，根据△AHC的面积+△DHC的面积=△ADC的面积求解即可．

∵四边形ABCD是矩形，且

∴B(-4,0)

∴AC=5

由作图知CH为∠ACD的平分线，过点H作HQ⊥AC，则HQ=HD，

∴△AHC的面积+△DHC的面积=△ADC的面积，

即：

∵HD=HQ

∴HD=3

∴点H的横坐标为：4-3=1．

故选：D．