题目内容
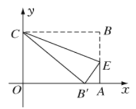
【题目】如图,在平面直角坐标系中放入一个一边长OC为9的矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为点B′,折痕为CE,已知tan∠OB′C=![]() .
.
(1)求点B′的坐标;
(2)求折痕CE所在直线的表达式.
【答案】(1)点B′的坐标为(12,0).(2)折痕CE所在直线的解析式为y=-![]() x+9
x+9
【解析】
对于(1),根据三角函数的定义,在Rt△B′OC中,结合tan∠OB′C=![]() ,求出OB′的长,从而得到点B′的坐标;
,求出OB′的长,从而得到点B′的坐标;
对于(2),根据折叠的性质可得△CBE≌△CB′E,则BE=B′E,CB′=CB=OA,由勾股定理求出CB′的长,再利用勾股定理求出AE的长,得到点E的坐标;再结合点C的坐标,利用待定系数法求出直线CE的解析式,问题即可得解.
(1)在Rt△B′OC中,tan∠OB′C=![]() ,OC=9,
,OC=9,
∴![]() =
=![]() ,解得OB′=12,
,解得OB′=12,
∴点B′的坐标为(12,0).
(2)将纸片翻折后,点B恰好落在x轴上的点B′处,CE为折痕,
∴△CBE≌△CB′E,
∴BE=B′E,CB′=CB=OA.
由勾股定理,得CB′=![]() =15.
=15.
设AE=a,则EB′=EB=9-a,
又AB′=AO-OB′=15-12=3,
∴由勾股定理,得a2+32=(9-a)2,
解得a=4,
∴点E的坐标为(15,4),
又点C的坐标为(0,9),
设直线CE的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴折痕CE所在直线的解析式为y=-![]() x+9
x+9

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目