��Ŀ����
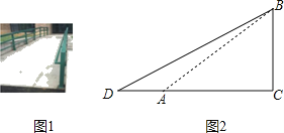
����Ŀ��������Сѩ��Ƶġ�������֪�߶�Ϊб�ߵĵ���ֱ�������Ρ��ij߹���ͼ���̣�
![]()
��֪���߶�AB��
��������ABΪб�ߵ�һ������ֱ�ǡ�ABC��
������
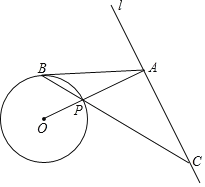
��1���ֱ��Ե�A�͵�BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶�����������ཻ��P��Q���㣻
AB�ij�Ϊ�뾶�����������ཻ��P��Q���㣻
��2����ֱ��PQ����AB�ڵ�O��
��3����OΪԲ�ģ�OA�ij�Ϊ�뾶��Բ����ֱ��PQ�ڵ�C��
��4������AC��BC��
���ABC��Ϊ�������������Σ�����Сѩ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�油ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤������PA=PB��QA=QB����PQ��ֱƽ��AB�� ��
�ڡ�O�У�
��ABΪֱ�������ACB=90�㣨 ��
�֡ߡ�AOC=��BOC=90�㣬��AC=BC�� �������ABCΪ��ABΪб�ߵĵ���ֱ�������Σ�
���𰸡���1���𰸼���������2�����߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�ֱ������Բ�ܽ���ֱ�ǣ���ȵ�Բ�Ľ����ԵĻ���ȡ����Ե�����ȣ�
��������
(1)��������������ֱ�ߺ�Բ�油ȫͼ�Σ�
(2)������ͼ���̼������֤����
(1)��ͼ��Ϊ��ȫ��ͼ�Σ�

(2)��������֤����
֤������PA=PB��QA=QB��
��PQ��ֱƽ��AB(���߶������˵������ȵĵ��������߶εĴ�ֱƽ������)
�ڡ�O�У�
��ABΪֱ����
���ACB=90�� (ֱ������Բ�ܽ���ֱ��)
�֡ߡ�AOC=��BOC=90�㣬
��AC=BC(��ȵ�Բ�Ľ����ԵĻ���ȡ����Ե������)��
���ABCΪ��ABΪб�ߵĵ���ֱ�������Σ�
�ʴ�Ϊ�����߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϡ�
ֱ������Բ�ܽ���ֱ�ǡ���ȵ�Բ�Ľ����ԵĻ���ȡ����Ե�����ȣ�

 53���ò�ϵ�д�
53���ò�ϵ�д�