��Ŀ����
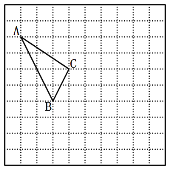
����Ŀ����ABC�͡�ADE�У�AB=AC��AD=AE����BAC=��DAE=����0�㣼����90�㣩����F��G��P�ֱ���DE��BC��CD���е㣬����PF��PG��
��1����ͼ�٣���=90�㣬��D��AB�ϣ����FPG= �㣻
��2����ͼ�ڣ���=60�㣬��D����AB�ϣ��жϡ�FPG�Ķ�������֤����Ľ��ۣ�
��3������FG����AB=5��AD=2���̶���ABC������ADE�Ƶ�A��ת����PF���ȵ����ֵΪ ��PF���ȵ���СֵΪ ��



��27��
���𰸡���1����GPF=90�㣻��2������FPG=120�㣬���������������3��![]() ��
��![]()
��������
��1����AB=AC��AD=AE���ó�BD=CE���ٸ���G��P��F�ֱ���BC��CD��DE���ص㣬���Եó�PG��BD,PF��CE.���GPF=180��-����=90��
(2)����BD��CE,����֪����֤����ABD�ա�ACE,���ABD=��ACE,��ΪG��P��F�ֱ���BC��CD��DE���е㣬��PG��BD,PF��CE,�����ó���GPF=180��-����=120��.
��3����D��BA���ӳ�����ʱ��CE=BD�����ʱBD=AB+AD=7;
��1����AB=AC��AD=AE��
��BD=CE��
��G��P��F�ֱ���BC��CD��DE���е㣬
��PG��BD��PF��CE��
���ADC=��DPG����DPF=��ACD��
���GPF=��DPF+��DPG=��ADC+��ACD=180��-��BAC=180��-����=90�㣬
����GPF=90�㣻
��2����FPG=120�����������£�

����BD������CE����ͼ��
�ߡ�BAC=��DAE��
���BAD=��CAE������ABD����ACE��

���ABD�ա�ACE��SAS����
���ABD=��ACE��
��G��P��F�ֱ���BC��CD��DE���е㣬
��PG��BD��PF��CE��
���PGC=��CBD����DPF=��DCE=��DCA+��ACE=��DCA+��ABD����DPG=��PGC+��BCD=��CBD+��BCD��
���GPF=��DPF+��DPG=��DCA+��ABD+��CBD+��BCD=180��-��BAC=180��-����=120�㣬
����GPF=120�㣻
��3��![]() ��
��![]()