题目内容
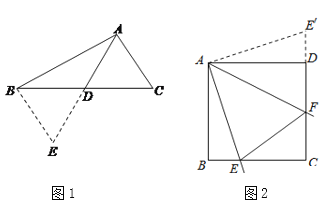
【题目】如图，在
中， 
，点
分别是
的中点， 
是
延长线上的一点，且
．
（1）求证： 
；
（2）求证： 
．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据三角形中位线定理可得DE=
BC，再根据
，从而可得DE=CF；
（2）利用SAS证明△BDE≌△ECF即可得.
试题解析：（1）∵点
分别是
的中点，
∴DE‖BC，且DE=
BC，
∵
，∴DE=CF；
（2）∵AD=BD=
AB，AE=EC=
AC，AB=AC，
∴BD=EC， AD=AE，
∴∠ADE=∠AED，
∴∠BDE=180°-∠ADE=180°-∠AED，
∵DE‖BC，∴∠AED=∠ACB，
∴∠ECF=180°-∠ACB ，∴∠BDE=∠ECF，
又由（1）得DE=CF， ∴△BDE≌△ECF（SAS），
∴BE=EF.
【题目】有这样一个问题:探究函数
的图象与性质.
小亮根据学习函数的经验，对函数的图象与性质进行了探究。
下面是小亮的探究过程，请补充完整:
(1)函数中自变量x的取值范围是_________.
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
|
| 2 | 3 | 4 | 5 | … |
y | … | - | - | -4 | -5 | -7 | m | -1 | -2 | - | - | … |
求m的值；
(3)在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
(4)根据画出的函数图象，发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交，该函数的图象还与直线_________越来越靠近而永不相交.
【题目】某果品超市经销一种水果，已知该水果的进价为每千克15元，通过一段时间的销售情况发现，该种水果每周的销售总额相同，且每周的销售量y（千克）与每千克售价x（元）的关系如表所示
每千克售价x（元） | 25 | 30 | 40 |
每周销售量y（千克） | 240 | 200 | 150 |
（1）写出每周销售量y（千克）与每千克售价x（元）的函数关系式；
（2）由于销售淡季即将来临，超市要完成每周销售量不低于300千克的任务，则该种水果每千克售价最多定为多少元？
（3）在（2）的基础上，超市销售该种水果能否到达每周获利1200元？说明理由．
