题目内容
【题目】阅读下列材料，然后解决问题：
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．
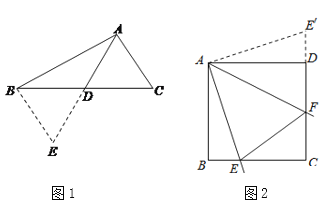
如图1，在△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可得4<ＡＥ<20 ，则2<AD<10.
（1）问题解决：受到上题解法的启发，如图2，在正方形ABCD中，已知：∠EAF=45°，角的两边AE、AF分别与BC、CD相交于点E、F，若BE=2，DF=3，求EF的长.可延长 CD到E′，使得DE′＝BE，连接AE′，先证△ABE≌△ADE′，进一步证明 △AEF≌△AE′F , 即可得EF=E′F, 那么EF=_________.
（2）问题拓展：
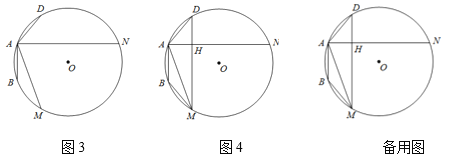
如图3，在⊙O中，AB、AD是⊙O的弦，且AB=AD，M、N是⊙O上的两点，∠MAN＝
∠BAD.
①如图4，连接MN、MD，求证：MH=BM+DH，DM⊥AN；
②若点C在
（点C不与点A、D、N重合）上，连接CB、CD分别交AM、AN或其延长线于点E、F，直接写出EF、BE、DF之间的等式关系.
【答案】（1）5；（2）①见解析，②EF＝BE+DF或DF＝EF+BE
【解析】
（1）根据题目给定的思路进行求解即可；
（2）①延长MD到点M′，使得DM′=BM，连接AM′，如图5．仿照材料中的证明思路可证到AM=AM′，∠MAN=∠M′AN，然后利用等腰三角形的性质即可解决问题．②分两种情况讨论：Ⅰ．当点C在
上时，如图1、2；Ⅱ．当点C在
上时，如图3．借鉴①中的证明思路就可得到结论．
（1）延长 CD到E′，使得DE′＝BE，连接AE′，
∵四边形ABCD是正方形，
∴AB=AB,∠B=∠ADC=90°，
∴∠AD E′=90°，
∵DE′＝BE，
∴△ABE≌△ADE′，
∴AE′=AE，∠BAE=∠DA E′
∴∠E′AE=90°,
∵∠EAF=45°，
∴∠E′AF=45°，
∴∠E′AF=∠EAF,
在△AEF和△AE′F中，
，
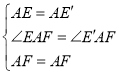∴ EF=E′F，
∵E′F=DE′+DF=BE+DF=2+3=5,
∴EF=5.
（2）①延长MD到点M′，使得DM′=BM，连接AM′，如图5．
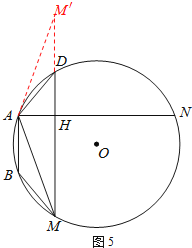
∵∠ADM′+∠ADM=180°，∠ABM+∠ADM=180°，
∴∠ABM=∠ADM′．
在△ABM和△ADM′中，
．
∴△ABM≌△ADM′（SAS）．
∴AM=AM′∠BAM=∠DAM′．
∴∠MAM′=∠BAD．
∵∠MAN=
∠BAD，
∴∠MAN=∠MAM′．
∴∠MAN=∠M′AN．
∵AM=AM′，∠MAN=∠M′AN，
∴MH=M′H，AH⊥MM′．
∴MH=M′H=DM′+DH=BM+DH，DM⊥AN．
②②Ⅰ．当点C在上时，如图1、2．
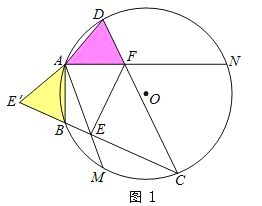
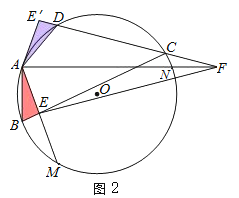
同理可得：EF=BE+DF．
Ⅱ．当点C在上时，如图3．
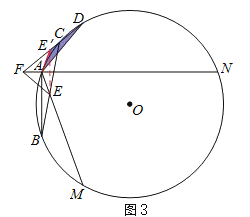
同理可得：DF＝EF+BE.．
