题目内容
【题目】在ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
【答案】见解析；菱形
【解析】试题分析：首先根据平行四边形的性质可得AD=BC，∠A=∠C，再加上条件AE=CF可利用SAS证明△ADE≌△CBF；首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论．
试题解析：（1）、∵四边形ABCD是平行四边形， ∴AD=BC，∠A=∠C，
∵在△ADE和△CBF中，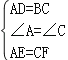
，∴△ADE≌△CBF（SAS）；
（2）、∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD， ∵AE=CF， ∴DF=EB，
∴四边形DEBF是平行四边形， 又∵DF=FB， ∴四边形DEBF为菱形．
练习册系列答案
阅读快车系列答案
相关题目
