题目内容
 如图,半圆的直径AB=10,点C在半圆上,BC=6.
如图,半圆的直径AB=10,点C在半圆上,BC=6.(1)求弦AC的长;
(2)把△BCE沿BE折叠,使点C与直径AB上的P点重合,连结PC.求PE,PC的长.
分析:(1)由AB是半圆的直径,得到∠ACB=90°,而AB=10,BC=6,根据勾股定理即可计算出AC;
(2)先根据轴对称的性质得出∠EPB=∠ACB=90°,PE=CE,BP=BC=6.设PE=x,则EC=x,AE=8-x,AP=4,再证明△APE∽△ACB,根据相似三角形的对应边成比例求出PE=3,再证明△PEF∽△BEP,根据相似三角形的对应边成比例求出PF=
.
(2)先根据轴对称的性质得出∠EPB=∠ACB=90°,PE=CE,BP=BC=6.设PE=x,则EC=x,AE=8-x,AP=4,再证明△APE∽△ACB,根据相似三角形的对应边成比例求出PE=3,再证明△PEF∽△BEP,根据相似三角形的对应边成比例求出PF=
12
| ||
| 5 |
解答:解:(1)∵AB是直径,
∴∠ACB=90°,
由勾股定理得,AC=8;
 (2)∵把△BCE沿BE折叠,点C与直径AB上的P点重合,
(2)∵把△BCE沿BE折叠,点C与直径AB上的P点重合,
∴△BCE≌△BPE,∠EPB=∠ACB=90°,PE=CE,BP=BC=6.
设PE=x,则EC=x,AE=8-x,AP=4.
∵在△APE与△ACB中,
,
∴△APE∽△ACB,
∴AP:AC=PE:CB,即4:8=x:6,
解得x=3,
∴PE=3,AE=5,BE=
=
=3
.
设PC与BE的交点为F.
∵P点C点关于BE对称,
∴BE是线段PC的垂直平分线,即BE⊥CP,PC=2PF.
∵在△PEF与△BEP中,
,
∴△PEF∽△BEP,
∴PF:BP=PE:BE,即PF:6=3:3
,
解得PF=
,
∴PC=2PF=
.
故PE=3,PC=
.
∴∠ACB=90°,
由勾股定理得,AC=8;
 (2)∵把△BCE沿BE折叠,点C与直径AB上的P点重合,
(2)∵把△BCE沿BE折叠,点C与直径AB上的P点重合,∴△BCE≌△BPE,∠EPB=∠ACB=90°,PE=CE,BP=BC=6.
设PE=x,则EC=x,AE=8-x,AP=4.
∵在△APE与△ACB中,
|
∴△APE∽△ACB,
∴AP:AC=PE:CB,即4:8=x:6,
解得x=3,
∴PE=3,AE=5,BE=
| BP2+PE2 |
| 62+32 |
| 5 |
设PC与BE的交点为F.
∵P点C点关于BE对称,
∴BE是线段PC的垂直平分线,即BE⊥CP,PC=2PF.
∵在△PEF与△BEP中,
|
∴△PEF∽△BEP,
∴PF:BP=PE:BE,即PF:6=3:3
| 5 |
解得PF=
6
| ||
| 5 |
∴PC=2PF=
12
| ||
| 5 |
故PE=3,PC=
12
| ||
| 5 |
点评:本题考查了圆周角定理,勾股定理,轴对称的性质,相似三角形的判定与性质,难度适中,根据两角对应相等的两三角形相似证明△APE∽△ACB及△PEF∽△BEP是解题的关键.

练习册系列答案
相关题目
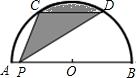 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于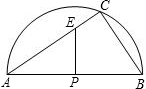 如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6.
如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6. (1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y=
(1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y= 如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )
如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )