Question

【题目】定义：如果一个三角形中有两个内角α，β满足α+2β＝90°，那我们称这个三角形为“近直角三角形”．

（1）若△ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝　 度；

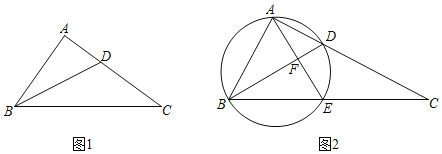
（2）如图1，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4．若BD是∠ABC的平分线，

①求证：△BDC是“近直角三角形”；

②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．

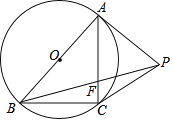
（3）如图2，在Rt△ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连结AE交BD于点F，若△BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值．

Answer 1

【答案】（1）20；（2）①见解析；②存在，CE＝；（3）tan∠C的值为或．

【解析】

（1）∠B不可能是α或β，当∠A＝α时，∠C＝β＝50°，α+2β＝90°，不成立；故∠A＝β，∠C＝α，α+2β＝90°，则β＝20°；

（2）①如图1，设∠＝ABD∠DBC＝β，∠C＝α，则α+2β＝90°，故△BDC是“近直角三角形”；

②∠ABE＝∠C，则△ABC∽△AEB，即,即，解得：AE=，即可求解.

（3）①如图2所示，当∠ABD＝∠DBC＝β时，设BH＝x，则HE＝5﹣x，则AH2＝AE2﹣HE2＝AB2﹣HB2，即52﹣x2＝62﹣（5﹣x）2，解得：x＝，即可求解；

②如图3所示，当∠ABD＝∠C＝β时，AF∶EF＝AG∶GE＝2∶3，则DE＝2k，则AG＝3k＝R（圆的半径）＝BG，点H是BE的中点，则GH＝DE＝k，在△BGH中，BH＝＝2k，在△ABH中，AB＝5，BH＝2k，AH＝AG+HG＝4k，由勾股定理得：25＝8k2+16k2，解得：k＝，即可求解.

解：（1）∠B不可能是α或β，

当∠A＝α时，∠C＝β＝50°，α+2β＝90°，不成立；

故∠A＝β，∠C＝α，α+2β＝90°，则β＝20°，

故答案为20；

（2）①如图1，设∠＝ABD∠DBC＝β，∠C＝α，

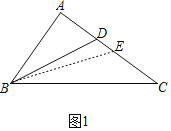
则α+2β＝90°，故△BDC是“近直角三角形”；

②存在，理由：

在边AC上是否存在点E（异于点D），使得△BCE是“近直角三角形”，

AB＝3，AC＝4，则BC＝5，

则∠ABE＝∠C，则△ABC∽△AEB，

即，即，解得：AE＝，

则CE＝4﹣＝；

（3）①如图2所示，当∠ABD＝∠DBC＝β时，

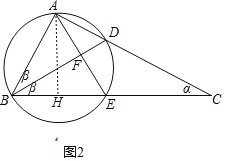
则AE⊥BF，则AF＝FE＝3，则AE＝6，

AB＝BE＝5，

过点A作AH⊥BC于点H，

设BH＝x，则HE＝5﹣x，

则AH2＝AE2﹣HE2＝AB2﹣HB2，即52﹣x2＝62﹣（5﹣x）2，解得：x＝；

cos∠ABE＝＝＝cos2β，则tan2β＝，

则tanα＝；

②如图3所示，当∠ABD＝∠C＝β时，

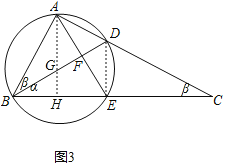
过点A作AH⊥BE交BE于点H，交BD于点G，则点G是圆的圆心（BE的中垂线与直径的交点），

∵∠AEB＝∠DAE+∠C＝α+β＝∠ABC，故AE＝AB＝5，则EF＝AE﹣AF＝5﹣3＝2，

∵DE⊥BC，AH⊥BC，

∴ED∥AH，则AF∶EF＝AG∶GE＝2∶3，

则DE＝2k，则AG＝3k＝R（圆的半径）＝BG，点H是BE的中点，则GH＝DE＝k，

在△BGH中，BH＝＝2k，

在△ABH中，AB＝5，BH＝2k，AH＝AG+HG＝4k，

由勾股定理得：25＝8k2+16k2，解得：k＝；

在△ABD中，AB＝5，BD＝6k＝，

则cos∠ABD＝cosβ＝＝＝cosC，

则tanC＝；

综上，tan∠C的值为或．