Question

（1）如图①，在正方形ABCD中，E、F分别是BC、CD上的点且∠EAF=45°．猜测线段EF、BE、FD三者存在哪种数量关系？直接写出结论．（不用证明）结论：________．
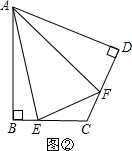
（2）如图②，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是BC、CD上的点，且∠EAF是∠BAD的一半．（1）中猜测的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；

Answer 1

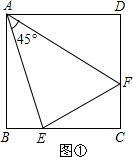
解：（1）延长CB到G，使BG=FD，

∵∠ABG=∠D=90°，AB=AD，
∴△ABG≌△ADF，
∴∠BAG=∠DAF，AG=AF，
∵∠EAF=∠BAD，
∴∠DAF+∠BAE=∠EAF，
∴∠EAF=∠GAE，
∴△AEF≌△AEG，
∴EF=EG=EB+BG=EB+DF．
故答案为：EF=BE+FD；

（2）结论成立，应为EF=BE+DF，
在CD的延长线上截取DG=BE，（如图）
∵BE=DG，AB=AD，
∠B=∠ADG=90°，
∴△ABE≌△ADG，
∴∠BAE=∠DAG，AG=AE，
∵∠EAF=∠BAD，
∴∠EAF=∠FAG，
AF=AF，AE=AG，
∴△AEF≌△AFG（SAS），
∴EF=FG=DF+DG=EB+DF．
分析：（1）延长CB到G，使BG=FD，根据已知条件容易证明△ABG≌△ADF，由此可以推出∠BAG=∠DAF，AG=AF，而∠EAF=∠BAD，所以得到∠DAF+∠BAE=∠EAF，进一步得到∠EAF=∠GAE，现在可以证明△AEF≌△AEG，然后根据全等三角形的性质就可以证明结论成立；
（2）在CD上截取DG=BE，利用BE=DG，AB=AD，∠B=∠ADG=90°，得出△ABE≌△ADG，进而得出△AEF≌△AFG即可得出答案．
点评：此题是开放性试题，首先在特殊图形中找到规律，然后再推广到一般图形中，对学生的分析问题，解决问题的能力要求比较高．