题目内容
给出下列四个命题：（1）将一个n（n≥4）边形的纸片剪去一个角，则剩下的纸片是n+1或n-1边形；（2）若
，则x=1或x=3；（3）若函数
是关于x的反比例函数，则
；（4）已知二次函数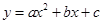
，且a＞0，a-b+c＜0,则
。其中，正确的命题有（ ）个.
| A．0 | B．1 | C．2 | D．4 |
B.
解析试题分析：（1）观察图形，分过两个顶点剪去一个角、过一个顶点或不过任何一个顶点剪去一个角作出的图形，找出减少的边数和增加的边数，然后根据多边形的定义即可得到剩下的是n+1或n-1、n，所以（1）不正确；（2）
，所以
，解得x=3，所以（2）不正确；（3）原式=
，所以2k-3=0,解得k=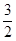
,正确；（4）由a-b+c＜0得
，代入
，所以（4）不正确
考点：1.多边形的性质；2.反比例函数的意义；3.二次函数的判别式.
练习册系列答案
考前必练系列答案
相关题目
如图，抛物线
和直线
. 当y1＞y2时，x的取值范围是（ ）
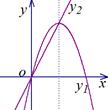
| A．0<x<2 | B．x<0或x＞2 | C．x<0或x＞4 | D．0<x<4 |
抛物线
与x轴的交点坐标是（ ）
| A．（1，0）（-3，0） | B．（-1，0）（3，0） |
| C．（1，0）（3，0） | D．（-1，0）（-3，0） |
二次函数y=ax2+bx+c（a≠0）中的x与y的部分对应值如下表：
| x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
（2）当
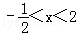时，y＜0；（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．
则其中正确结论的个数是（ ）
A．1个 B．2个 C． 3个 D．0个
将二次函数
的图象向右平移2个单位后，所得图象的函数表达式是（ ）
A． | B． | C． | D． |
抛物线y＝a（x＋1）（x－3）（a≠0）的对称轴是直线（ ）
| A．x＝1 | B．x＝－1 | C．x＝－3 | D．x＝3 |
函数
与
在同一坐标系中的大致图象是（ ）
A． | B． | C． | D． |
二次函数y=ax2+bx+c的y与x的部分对应值如下表
| x | … | 0 | 1 | 3 | 4 | … |
| y | … | 2 | 4 | 2 | －2 | … |
A、抛物线开口向上
B、抛物线与y轴交于负半轴
C、当x=－1时y＞0
D、方程ax2+bx+c=0的负根在0与－1之间
直角坐标平面上将二次函数y=x2﹣2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ）
| A．（0，0） | B．（1，﹣1） | C．（0，﹣1） | D．（﹣1，﹣1） |