题目内容
【题目】已知:![]() ,
,![]() 是圆
是圆![]() 的两条直径,连接
的两条直径,连接![]() ,
,![]() .
.
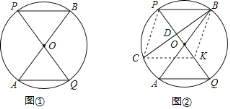
![]() 如图①,求证:
如图①,求证:![]() ,
,![]() ;
;
![]() 如图②,过点
如图②,过点![]() 作
作![]() 于点
于点![]() ,交圆
,交圆![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
求证:四边形![]() 是平行四边形.
是平行四边形.

【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)由同弧所对的圆周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根据∠AOQ=∠BOP,得到![]() ,那么AQ=BP;
,那么AQ=BP;
(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
证明:![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() ∵
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 与
与![]() 互相垂直且平分,
互相垂直且平分,
∴四边形![]() 为菱形;
为菱形;
∴![]() ,且
,且![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
相关题目






