题目内容
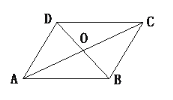
【题目】已知□ABCD的对角线AC与BD交于点O,求证:AB2+BC2+CD2+DA2=AC2+BD2.
【答案】证明见解析
【解析】
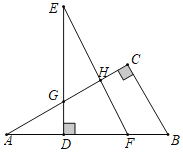
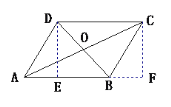
如图,过点O、C分别作DE⊥AB,CF⊥AB,E、F为垂足,运用勾股定理求证即可.
如图,过点O、C分别作DE⊥AB,CF⊥AB,E、F为垂足
又四边形ABCD是平行四边形
∴△ADE≌△BCF
∴AE=BF AB=EF=CD
∴AD2+BC2=AE2+DE2+BF2+CF2
AC2+BD2=AF2+CF2+DE2+BE2
=(AB+BF)2+CF2+DE2+(AB-AE)2
=(AB+BF)2+CF2+DE2+(AB-BF)2
=2AB2+2BF2+CF2+DE2
=AB2+CD2+BF2+AE2+CF2+DE2
=AB2+CD2+AD2+BC2

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目