题目内容
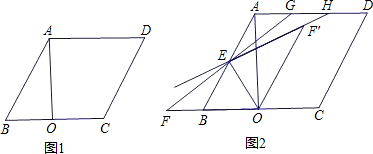
如图1,在?ABCD中,AO⊥BC,垂足为O,已知∠ABC=60°,BO=2,AO=2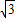 .
.(1)求线段AB的长;
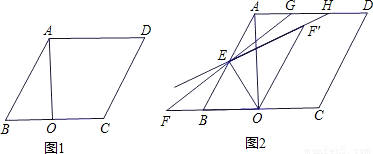
(2)如图2,点E为线段AB的中点,过点E的直线FG与CB的延长线交于点F,与射线AD交于点G,连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF′,记直线EF′与射线AD的交点为H.
①当点G在点H的左侧时,求证:△AEG∽△AHE;
②若HG=6,求AG的长.
【答案】分析:(1)直接利用勾股定理可求AB;(2)①由于AD∥CF,∠F=∠AGE,∠F=∠EF′O,OB=BE=2,∠ABC=60°,易证△BOE是等边三角形,那么∠EOF′=60°,∠F′OC=60°,于是OF′∥AB,根据平行线的性质可知∠AEH=∠EF′O,易证△AEG∽△AHE;②由①中,△AEG∽△AHE可得AE:AH=AG:AE,
设AG=x,再分情况讨论,一种是点H在点G的右侧时;另一种是点H在点G的左侧时,分别计算即可.
解答:解:(1)∵AO⊥BC,BO=2,AO=2 ,
,
∴AB=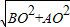 =
=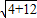 =4;
=4;
(2)①证明:AD∥CF,∠F=∠AGE,∠F=∠EF′O,OB=BE=2,∠ABC=60°,
∴△BOE是等边三角形,
∴∠EOF′=60°,∠F′OC=60°,
∴OF′∥AB,
∴∠AEH=∠EF′O,
∴∠AEH=∠AGE,∠EAG=∠EAG,
∴△AEG∽△AHE;
②由①知△AEG∽△AHE,
∴AE:AH=AG:AE,
即AE2=AH•AG,设AG=x,
当点H在点G的右侧时,
∴4=x(x+6),
解得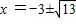 取
取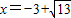 ;
;
当点H在点G的左侧时,
∴4=x(x-6),
解得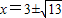 ,取
,取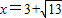 .
.
点评:本题考查了勾股定理、等边三角形的判定和性质、相似三角形的判定和性质、平行线的判定和性质、分情况讨论、解一元二次方程.
设AG=x,再分情况讨论,一种是点H在点G的右侧时;另一种是点H在点G的左侧时,分别计算即可.
解答:解:(1)∵AO⊥BC,BO=2,AO=2
 ,
,∴AB=
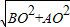 =
=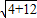 =4;
=4;(2)①证明:AD∥CF,∠F=∠AGE,∠F=∠EF′O,OB=BE=2,∠ABC=60°,
∴△BOE是等边三角形,
∴∠EOF′=60°,∠F′OC=60°,
∴OF′∥AB,
∴∠AEH=∠EF′O,
∴∠AEH=∠AGE,∠EAG=∠EAG,
∴△AEG∽△AHE;
②由①知△AEG∽△AHE,
∴AE:AH=AG:AE,
即AE2=AH•AG,设AG=x,
当点H在点G的右侧时,
∴4=x(x+6),
解得
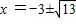 取
取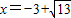 ;
;当点H在点G的左侧时,
∴4=x(x-6),
解得
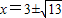 ,取
,取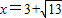 .
.点评:本题考查了勾股定理、等边三角形的判定和性质、相似三角形的判定和性质、平行线的判定和性质、分情况讨论、解一元二次方程.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目



 )时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
)时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.