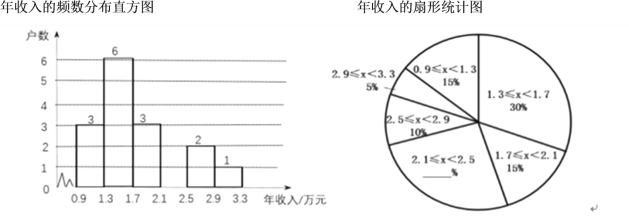
题目内容
【题目】在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________度.
【答案】60或10
【解析】
先由三角形内角和算出∠ACB,△ACD为直角三角形,分别讨论当∠ADC=90°和∠ACD=90°时,算出即可.
解:∵ △ABC中,∠A=50°,∠B=30°,
∴∠ACB=180°-∠A-∠B=180°-50°-30°=100°,
点D在AB边上, △ACD为直角三角形,
①如图所示,当∠ADC=90°时,∠ACD=90°-∠A=90°-50°=40°,
∴∠BCD=∠ACB-∠ACD=100°-40°=60°;

②如图所示,当∠ACD=90°时,∠BCD=∠ACB-∠ACD=100°-90°=10°;
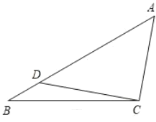
故答案为:60°或10°

练习册系列答案
相关题目