题目内容
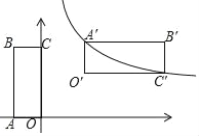
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )
A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
【答案】C
【解析】
设A'(a,![]() ),则C'(a+2,
),则C'(a+2,![]() -1),依据反比例函数图象上点的坐标特征,即可得到a=2,进而得出A'(2,2),C'(4,1),设P(x,y),再根据AP=A'P,CP=C'P,即可得到方程组
-1),依据反比例函数图象上点的坐标特征,即可得到a=2,进而得出A'(2,2),C'(4,1),设P(x,y),再根据AP=A'P,CP=C'P,即可得到方程组![]() ,进而得出旋转中心P点的坐标.
,进而得出旋转中心P点的坐标.
解:如图,
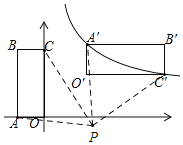
∵B的坐标为(-1,2),
∴矩形的长为2,宽为1,
由旋转可得,A'O'⊥x轴,O'C'⊥y轴,
设A'(a,![]() ),则C'(a+2,
),则C'(a+2,![]() -1),
-1),
∵点C'在反比例函数y=![]() 的图象上,
的图象上,
∴(a+2)(![]() -1)=4,
-1)=4,
解得a=2(负值已舍去),
∴A'(2,2),C'(4,1),
由旋转的性质可得,AP=A'P,CP=C'P,
设P(x,y),则
![]() ,
,
解得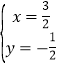 ,
,
∴旋转中心P点的坐标是(![]() ,-
,-![]() ),
),
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目