题目内容
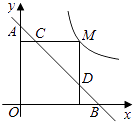
【题目】如图,函数y= ![]() 和y=﹣
和y=﹣ ![]() 的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 . 
【答案】8
【解析】解:∵点P在y= ![]() 上,
上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a, ![]() )(a为正数),
)(a为正数),
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=﹣ ![]() 上,
上,
∴A的坐标是(a,﹣ ![]() ),
),
∵PB⊥y轴,
∴B的纵坐标是 ![]() ,
,
∵B在y=﹣ ![]() 上,
上,
∴代入得: ![]() =﹣
=﹣ ![]() ,
,
解得:x=﹣3a,
∴B的坐标是(﹣3a, ![]() ),
),
∴PA=| ![]() ﹣(﹣
﹣(﹣ ![]() )|=
)|= ![]() ,
,
PB=|a﹣(﹣3a)|=4a,
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是: ![]() PA×PB=
PA×PB= ![]() ×
× ![]() ×4a=8.
×4a=8.
所以答案是:8.
【考点精析】掌握比例系数k的几何意义是解答本题的根本,需要知道几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
相关题目