题目内容
【题目】已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0），且a＜b．
（Ⅰ）求抛物线顶点Q的坐标（用含a的代数式表示）；
（Ⅱ）说明直线与抛物线有两个交点；
（Ⅲ）直线与抛物线的另一个交点记为N．
（ⅰ）若﹣1≤a≤﹣ 
，求线段MN长度的取值范围；
（ⅱ）求△QMN面积的最小值．
【答案】解：（Ⅰ）∵抛物线y=ax2+ax+b过点M（1，0），
∴a+a+b=0，即b=﹣2a，
∴y=ax2+ax+b=ax2+ax﹣2a=a（x+ 
）2﹣ 
，
∴抛物线顶点Q的坐标为（﹣ ，﹣ ）；
（Ⅱ）∵直线y=2x+m经过点M（1，0），
∴0=2×1+m，解得m=﹣2，
联立直线与抛物线解析式，消去y可得ax2+（a﹣2）x﹣2a+2=0（*）
∴△=（a﹣2）2﹣4a（﹣2a+2）=9a2﹣12a+4，
由（Ⅰ）知b=﹣2a，且a＜b，
∴a＜0，b＞0，
∴△＞0，
∴方程（*）有两个不相等的实数根，
∴直线与抛物线有两个交点；
（Ⅲ）联立直线与抛物线解析式，消去y可得ax2+（a﹣2）x﹣2a+2=0，即x2+（1﹣ 
）x﹣2+ =0，
∴（x﹣1）[x﹣（ ﹣2）]=0，解得x=1或x= ﹣2，
∴N点坐标为（ ﹣2， 
﹣6），
（i）由勾股定理可得MN2=[（ ﹣2）﹣1]2+（ ﹣6）2= 
﹣ 
+45=20（ 
﹣ 
）2 ，
∵﹣1≤a≤﹣ ，
∴﹣2≤ ≤﹣1，
∴MN2随 的增大而减小，
∴当 =﹣2时，MN2有最大值245，则MN有最大值7 
，
当 =﹣1时，MN2有最小值125，则MN有最小值5 ，
∴线段MN长度的取值范围为5 ≤MN≤7 ；
（ii）如图，设抛物线对称轴交直线与点E，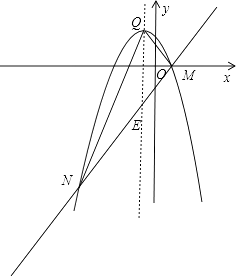
∵抛物线对称轴为x=﹣ ，
∴E（﹣ ，﹣3），
∵M（1，0），N（ ﹣2， ﹣6），且a＜0，设△QMN的面积为S，
∴S=S△QEN+S△QEM= |（ ﹣2）﹣1||﹣ ﹣（﹣3）|= 
﹣ 
﹣ 
，
∴27a2+（8S﹣54）a+24=0（*），
∵关于a的方程（*）有实数根，
∴△=（8S﹣54）2﹣4×27×24≥0，即（8S﹣54）2≥（36 
）2 ，
∵a＜0，
∴S= ﹣ ﹣ ＞ ，
∴8S﹣54＞0，
∴8S﹣54≥36 ，即S≥ + 
，
当S= + 时，由方程（*）可得a=﹣ 
满足题意，
∴当a=﹣ ，b= 
时，△QMN面积的最小值为 + ．
【解析】（Ⅰ）把M点坐标代入抛物线解析式可得到b与a的关系，可用a表示出抛物线解析式，化为顶点式可求得其顶点坐标；（Ⅱ）由直线解析式可先求得m的值，联立直线与抛物线解析式，消去y，可得到关于x的一元二次方程，再判断其判别式大于0即可；（Ⅲ）（i）由（Ⅱ）的方程，可求得N点坐标，利用勾股定理可求得MN2 ， 利用二次函数性质可求得MN长度的取值范围；（ii）设抛物线对称轴交直线与点E，则可求得E点坐标，利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积，再整理成关于a的一元二次方程，利用判别式可得其面积的取值范围，可求得答案．
