题目内容
(2006•攀枝花)已知等腰△ABC的腰AB=AC=10cm,底边BC=12cm,则△ABC的角平分线AD的长是 cm.
【答案】分析:由已知可以得到等腰三角形被它的顶角的平分线,平分成两个全等的直角三角形,可以利用勾股定理来求解.
解答: 解:如图,由等腰三角形的“三线合一”性质,知AD⊥BC,且BD=CD,
解:如图,由等腰三角形的“三线合一”性质,知AD⊥BC,且BD=CD,
在Rt△ABD中,
∵AB=10,BD= BC=6,
BC=6,
∴AD= =
=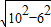 =8(cm).
=8(cm).
故应填8.
点评:命题立意:此题主要考查等腰三角形的“三线合一”性质及勾股定理.
解答:
 解:如图,由等腰三角形的“三线合一”性质,知AD⊥BC,且BD=CD,
解:如图,由等腰三角形的“三线合一”性质,知AD⊥BC,且BD=CD,在Rt△ABD中,
∵AB=10,BD=
 BC=6,
BC=6,∴AD=
 =
=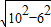 =8(cm).
=8(cm).故应填8.
点评:命题立意:此题主要考查等腰三角形的“三线合一”性质及勾股定理.

练习册系列答案
相关题目
 .
.