题目内容
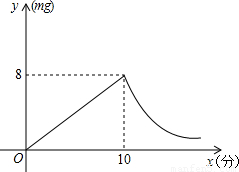
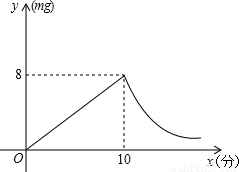
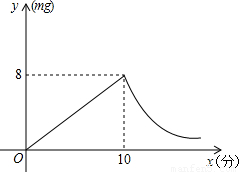
(2006•攀枝花)某人采用药熏法进行室内消毒,已知药物燃烧时室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物10分钟燃完,此时室内空气中每立方米的含药量为8毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y与x的函数关系式为______,自变量x的取值范围是______;药物燃烧后,y与x的函数关系式为______.
(2)研究表明,当空气中每立方米的含药量低于2毫克时,人方可进入室内,那么从消毒开始,至少需要经过______分钟后,人才可以回到室内.
(3)当空气中每立方米的含药量不低于5毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效,为什么?
【答案】分析:(1)分别根据题意利用待定系数法可求得函数的解析式;
(2)分别把题意中对应的变量的值代入对应的函数解析式中求出未知数的值;
(3)在计算的时候要注意要把y=5分别代入两个函数解析式,从而求得时间差.
解答:解:(1)药物燃烧时,y与x的函数关系式为y= x,
x,
自变量x的取值范围是0≤x≤10,
药物燃烧后,y与x的函数关系式为y= ;
;
(2)当y=2时,x=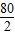 =40,
=40,
∴从消毒开始,至少需要经过40分钟后,人才可以回到室内;
(3)药物燃烧时,y与x的函数关系式为y= x,
x,
当y=5时,x=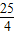 ;
;
药物燃烧后,y与x的函数关系式为y= ,y=5时,x=16,
,y=5时,x=16,
而空气中每立方米的含药量不低于5毫克的持续时间为: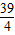 <10.
<10.
所以,此次消毒无效.
点评:主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.注意此题是分段函数,其自变量的值是连续的.
(2)分别把题意中对应的变量的值代入对应的函数解析式中求出未知数的值;
(3)在计算的时候要注意要把y=5分别代入两个函数解析式,从而求得时间差.
解答:解:(1)药物燃烧时,y与x的函数关系式为y=
 x,
x,自变量x的取值范围是0≤x≤10,
药物燃烧后,y与x的函数关系式为y=
 ;
;(2)当y=2时,x=
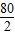 =40,
=40,∴从消毒开始,至少需要经过40分钟后,人才可以回到室内;
(3)药物燃烧时,y与x的函数关系式为y=
 x,
x,当y=5时,x=
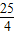 ;
;药物燃烧后,y与x的函数关系式为y=
 ,y=5时,x=16,
,y=5时,x=16,而空气中每立方米的含药量不低于5毫克的持续时间为:
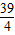 <10.
<10.所以,此次消毒无效.
点评:主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.注意此题是分段函数,其自变量的值是连续的.

练习册系列答案
相关题目
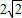 .
.