题目内容
(2006•攀枝花)已知抛物线y=ax2+bx+c与y轴的交点为C,顶点为M,直线CM的解析式y=-x+2并且线段CM的长为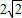 .
.(1)求抛物线的解析式;
(2)设抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在B的左侧,求线段AB的长;
(3)若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由.
【答案】分析:(1)利用C为抛物线和直线的公共点,根据直线解析式可求得C点坐标,进而求出c的值;利用M为抛物线和直线的公共点,将抛物线顶点坐标代入直线,求出b的值;过M点作y轴的垂线,垂足为Q,构造直角三角形,利用勾股定理求出a的值;
(2)依据两点之间距离公式求解即可.已知抛物线与x轴有两个交点,故求出抛物线应为:y=- x2-2x+2.抛物线与x轴有两个交点且点A在B的左侧,故|AB|=|x1-x2|=4
x2-2x+2.抛物线与x轴有两个交点且点A在B的左侧,故|AB|=|x1-x2|=4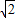 ;
;
(3)求出⊙N半径和直线到圆心的距离,比较它们的大小即可判断其位置关系.
解答: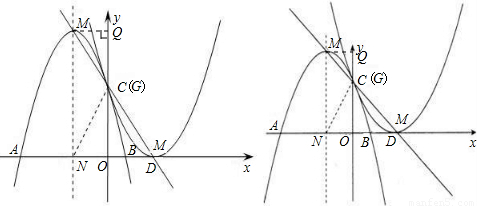
解:(1)解法一:
由已知,直线CM:y=-x+2与y轴交于点C(0,2)
抛物线y=ax2+bx+c过点C(0,2),
所以c=2,抛物线y=ax2+bx+c的顶点M(-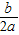 ,
,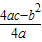 )在直线CM上,
)在直线CM上,
所以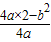 =
= +2,
+2,
解得b=0或b=-2(2分)
若b=0,点C、M重合,不合题意,舍去,
所以b=-2.即M(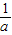 ,2-
,2- )
)
过M点作y轴的垂线,垂足为Q,
在Rt△CMQ中,CM2=CQ2+QM2
所以,8=( )2+[2-(2-
)2+[2-(2- )]2,
)]2,
解得,a=± .
.
∴所求抛物线为:y=- x2-2x+2或y=
x2-2x+2或y= x2-2x+2(4分)
x2-2x+2(4分)
以下同下.
解法二:由题意得C(0,2),
设点M的坐标为M(x,y)
∵点M在直线y=-x+2上,
∴y=-x+2
由勾股定理得CM=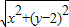 ,
,
由勾股定理得CM=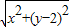 ,
,
∵CM=2 ,即x2+(y-2)2=8
,即x2+(y-2)2=8
解方程组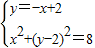
得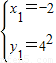 ,
,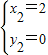 (2分)
(2分)
∴M(-2,4)或M‘(2,0)
当M(-2,4)时,
设抛物线解析式为y=a(x+2)2+4,
∵抛物线过(0,2)点,
∴a=- ,
,
∴y=- x2-2x+2(3分)
x2-2x+2(3分)
当M‘(2,0)时,
设抛物线解析式为y=a(x-2)2
∵抛物线过(0,2)点,
∴a= ,
,
∴y=- x2-2x+2
x2-2x+2
∴所求抛物线为:y=- x2-2x+2或y=
x2-2x+2或y= x2-2x+2(4分);
x2-2x+2(4分);
(2)∵抛物线与x轴有两个交点,
∴y= x2-2x+2不合题意,舍去.
x2-2x+2不合题意,舍去.
∴抛物线应为:y=- x2-2x+2(6分)
x2-2x+2(6分)
抛物线与x轴有两个交点且点A在B的左侧,
∴y=- x2-2x+2=0,
x2-2x+2=0,
得AB=|x1-x2|= =4
=4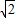 ;(8分)
;(8分)
(3)∵AB是⊙N的直径,
∴r=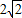 ,N(-2,0),
,N(-2,0),
又∵M(-2,4),
∴MN=4
设直线y=-x+2与x轴交于点D,则D(2,0),
∴DN=4,可得MN=DN,
∴∠MDN=45°,作NG⊥CM于G,在Rt△NGD中,
NG=DN•sin45°=2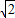 =r(10分)
=r(10分)
即圆心到直线CM的距离等于⊙N的半径
∴直线CM与⊙N相切(12分).
点评:此题作为压轴题,综合考查了二次函数及圆的相关知识.本题综合性较强,综合了函数、方程、圆等知识,解第3小题时可以根据图形的直观对结论进行猜想再证明.
(2)依据两点之间距离公式求解即可.已知抛物线与x轴有两个交点,故求出抛物线应为:y=-
 x2-2x+2.抛物线与x轴有两个交点且点A在B的左侧,故|AB|=|x1-x2|=4
x2-2x+2.抛物线与x轴有两个交点且点A在B的左侧,故|AB|=|x1-x2|=4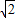 ;
;(3)求出⊙N半径和直线到圆心的距离,比较它们的大小即可判断其位置关系.
解答:

解:(1)解法一:
由已知,直线CM:y=-x+2与y轴交于点C(0,2)
抛物线y=ax2+bx+c过点C(0,2),
所以c=2,抛物线y=ax2+bx+c的顶点M(-
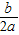 ,
,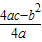 )在直线CM上,
)在直线CM上,所以
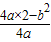 =
= +2,
+2,解得b=0或b=-2(2分)
若b=0,点C、M重合,不合题意,舍去,
所以b=-2.即M(
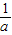 ,2-
,2- )
)过M点作y轴的垂线,垂足为Q,
在Rt△CMQ中,CM2=CQ2+QM2
所以,8=(
 )2+[2-(2-
)2+[2-(2- )]2,
)]2,解得,a=±
 .
.∴所求抛物线为:y=-
 x2-2x+2或y=
x2-2x+2或y= x2-2x+2(4分)
x2-2x+2(4分)以下同下.
解法二:由题意得C(0,2),
设点M的坐标为M(x,y)
∵点M在直线y=-x+2上,
∴y=-x+2
由勾股定理得CM=
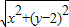 ,
,由勾股定理得CM=
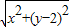 ,
,∵CM=2
 ,即x2+(y-2)2=8
,即x2+(y-2)2=8解方程组
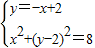
得
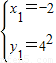 ,
,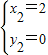 (2分)
(2分)∴M(-2,4)或M‘(2,0)
当M(-2,4)时,
设抛物线解析式为y=a(x+2)2+4,
∵抛物线过(0,2)点,
∴a=-
 ,
,∴y=-
 x2-2x+2(3分)
x2-2x+2(3分)当M‘(2,0)时,
设抛物线解析式为y=a(x-2)2
∵抛物线过(0,2)点,
∴a=
 ,
,∴y=-
 x2-2x+2
x2-2x+2∴所求抛物线为:y=-
 x2-2x+2或y=
x2-2x+2或y= x2-2x+2(4分);
x2-2x+2(4分);(2)∵抛物线与x轴有两个交点,
∴y=
 x2-2x+2不合题意,舍去.
x2-2x+2不合题意,舍去.∴抛物线应为:y=-
 x2-2x+2(6分)
x2-2x+2(6分)抛物线与x轴有两个交点且点A在B的左侧,
∴y=-
 x2-2x+2=0,
x2-2x+2=0,得AB=|x1-x2|=
 =4
=4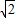 ;(8分)
;(8分)(3)∵AB是⊙N的直径,
∴r=
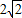 ,N(-2,0),
,N(-2,0),又∵M(-2,4),
∴MN=4
设直线y=-x+2与x轴交于点D,则D(2,0),
∴DN=4,可得MN=DN,
∴∠MDN=45°,作NG⊥CM于G,在Rt△NGD中,
NG=DN•sin45°=2
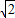 =r(10分)
=r(10分)即圆心到直线CM的距离等于⊙N的半径
∴直线CM与⊙N相切(12分).
点评:此题作为压轴题,综合考查了二次函数及圆的相关知识.本题综合性较强,综合了函数、方程、圆等知识,解第3小题时可以根据图形的直观对结论进行猜想再证明.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目