题目内容
【题目】(1)在△ABC中,∠BAC=60°,BC=4![]() ,则△ABC面积的最大值是 .
,则△ABC面积的最大值是 .
(2)已知:△ABC,用无刻度的直尺和圆规求作△DBC,使∠BDC+∠A=180°,且BD=DC.(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注,作出一个符合题意的三角形即可)
【答案】(1)12![]() ;(2)如图所示见解析.
;(2)如图所示见解析.
【解析】
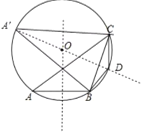
(1)作AB、BC的垂直平分线,它们相交于点O,再以点O为圆心,OA为半径作圆得到△ABC的外接圆,利用三角形面积公式得到当点A到BC的距离最大时,△ABC面积的最大,此时点A在优弧BC的中点,利用圆周角定理可判断△A′BC为等边三角形,然后利用等边三角形的面积的计算方法可得到△ABC面积的最大值;
(2)BC的垂直平分线交BC弧于D,根据垂径定理得到弧BD=弧CD,根据圆周角定理得到∠BDC+∠A=180°,从而可判断△DBC满足条件.
解:(1)作△ABC的外接圆⊙O,
当点A到BC的距离最大时,△ABC面积的最大,此时点A在BC的垂直平分线上,
如图,点A在A′时△ABC的面积最大,
∵∠BA′C=∠BAC=60°,
A′B=A′C,
∴△A′BC为等边三角形,
∴△ABC面积的最大值=![]() ×(4
×(4![]() )2=12
)2=12![]()
故答案为12![]() ,
,
(2)如图,△DBC为所作.

练习册系列答案
相关题目