题目内容
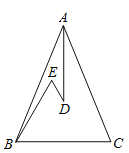
【题目】如图,在![]() 中,
中,![]() 是
是![]() 内两点,
内两点,![]() 平分
平分![]()
![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____________
____________![]() .
.
【答案】12
【解析】
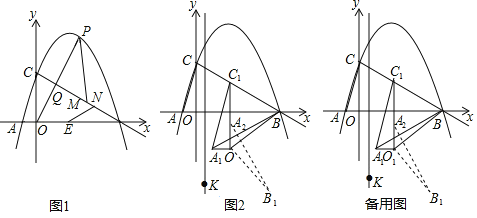
首先延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,易得:△EFD∽△EBM,又由AB=AC,AD平分∠BAC,根据等腰三角形的性质,即可得AN⊥BC,BN=CN,又由∠EBC=∠E=60°,可得△BEM与△EFD为等边三角形,又由直角三角形中,30°角所对的直角边是斜边的一半,即可求得MN与BM的值,继而求得答案.
解:延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,
∴△EFD∽△EBM,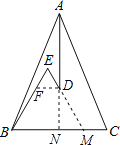
∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∴△EFD为等边三角形,
∵BE=9cm,DE=3cm,
∴DM=6cm,
∵∠DNM=90°,∠DMN=60°,
∴∠NDM=30°,
∴NM=![]() DM=3cm,
DM=3cm,
∴BN=BM-MN=9-3=6(cm),
∴BC=2BN=12(cm).

练习册系列答案
相关题目