题目内容
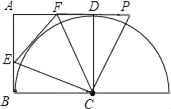
【题目】如图,在正方形ABCD中,E是AB边上任意一点,∠ECF=45°,CF交AD于点F,将△CBE绕点C顺时针旋转到△CDP,点P恰好在AD的延长线上.
(1)求证:EF=PF;
(2)直线EF与以C为圆心,CD为半径的圆相切吗?为什么?
【答案】(1)见解析;(2)相切.理由见解析.
【解析】
(1)根据已知判定△ECF≌△PCF,从而得到EF=PF;
(2)过点C作CQ⊥EF于点Q,由(1)得,△ECF≌△PCF又CQ⊥EF,CD⊥FP,根据切线的判定定理,从而得到直线EF与以C为圆心,CD为半径的圆相切.
(1)在正方形ABCD中,∠BCD=90°,
依题意△CDP是△CBE绕点C旋转90°得到,
∴∠ECP=90°,CE=CP,
∵∠ECF=45°,
∴∠FCP=∠ECP﹣∠ECF=90°﹣45°=45°,
∴∠ECF=∠FCP,CF=CF,
∴△ECF≌△PCF,
∴EF=PF;
(2)相切.理由如下:
过点C作CQ⊥EF于点Q,
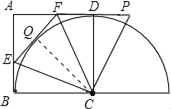
由(1)得,△ECF≌△PCF,
∴∠EFC=∠PFC,
∵CQ⊥EF,CD⊥FP,
∴CQ=CD,
∴直线EF与以C为圆心,CD为半径的圆相切.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目