��Ŀ����
����Ŀ����ij�����ٹ�·BC��(��·��Ϊֱ��)����ͨ�������Ź涨�����������ʻ�ٶȲ��ܳ���60 km/h����![]() ����������ù�·100 m��������һ������A.����ͼ��ƽ��ֱ������ϵ�У���Aλ��y���ϣ�����·��BC��x���ϣ���B�ڵ�A�ı�ƫ��60�㷽���ϣ���C�ڵ�A�ı�ƫ��45�㷽���ϣ�����һ����·��y���ϣ�AOΪ���е�һ�Σ�
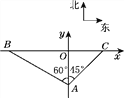
����������ù�·100 m��������һ������A.����ͼ��ƽ��ֱ������ϵ�У���Aλ��y���ϣ�����·��BC��x���ϣ���B�ڵ�A�ı�ƫ��60�㷽���ϣ���C�ڵ�A�ı�ƫ��45�㷽���ϣ�����һ����·��y���ϣ�AOΪ���е�һ�Σ�
(1)���B�͵�C�����ꣻ
(2)һ�������ӵ�B������ʻ����C���õ�ʱ����15 s��ͨ�����㣬�жϸ��������������·���Ƿ��٣�(�ο����ݣ� ![]() ��1.7)
��1.7)
���𰸡�������
���������������:���ݷ�λ�ǵĸ���,�ó���BAO=60��,��CAO=45��,����BAO=60���ɵ���ABO=30��,�����ɵ�AB��ֵ,Ȼ����Rt��ABO���ɹ��ɶ��������OB��ֵ,��2���ж��Ƿ��پ�����BC�ij�,Ȼ��Ƚϼ���.
�⣺(1)��Rt��AOB�У�
�ߡ�BAO��60�������ABO��30������OA��![]() AB.
AB.
��OA��100 m����AB��200 m.
�ɹ��ɶ�������OB��![]() ��100
��100![]() (m)��
(m)��
��Rt��AOC�У��ߡ�CAO��45�㣬���OCA����OAC��45��.
��OC��OA��100 m����B(��100![]() ��0)��C(100��0)��
��0)��C(100��0)��
(2)��BC��BO��CO��(100![]() ��100)m��
��100)m�� ![]() ��18>
��18>![]() ��
��
���������������ˣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
