Question

【题目】如图，正比例函数y=-3x的图象与反比例函数y=的图象交于A、B两点，点C在x轴负半轴上，AC＝AO，△ACO的面积为12．

（1）求k的值；

（2）根据图象，当y<y时，写出自变量x的取值范围.

Answer 1

【答案】（1）k=-12 ；（2）由图像可知： 当y>y时，x<-2或0<x<2.

【解析】试题分析：（1）过点A作AD⊥CO于点D，因为AC=CO，所以DC=DO，所以不难求出△ADO的面积，根据k的几何意义即可求出k；（2）求出一次函数和反比例函数的交点坐标，根据图像判断出x的范围即可.

试题解析：

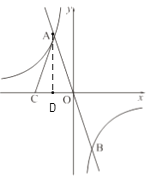
（1）过点A作AD⊥CO于点D，

∴AC=AO，

∴CD=DO= OC，

∴S△AOC=OC·AD=12，

∴OD·AD=12，

∴k=－12 ；

（2）y1=－3x，y2=－，

令y1=y2，－3x=－，解得x1=－2，x2=2，

由图像可知： 当y1>y2时，x<－2或0<x<2.