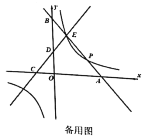
题目内容
【题目】我们把对角线互相垂直的四边形叫做垂直四边形.
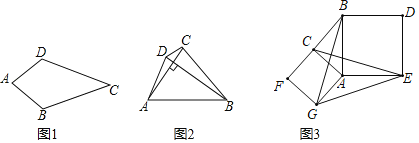
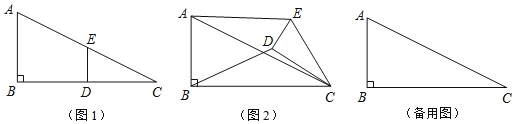
(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;
(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;
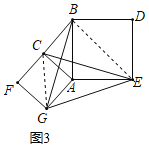
(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.
【答案】(1)四边形ABCD是垂直四边形;理由见解析;(2)见解析;(3)GE=![]()
【解析】
(1)由AB=AD,得出点A在线段BD的垂直平分线上,由CB=CD,得出点C在线段BD的垂直平分线上,则直线AC是线段BD的垂直平分线,即可得出结果;
(2)设AC、BD交于点E,由AC⊥BD,得出∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+DE2+CE2,即可得出结论;
(3)连接CG、BE,由正方形的性质得出AG=AC,AB=AE,![]() ,
,![]() ,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,推出∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,得出四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,
,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,推出∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,得出四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,![]() ,
,![]() ,代入计算即可得出结果.
,代入计算即可得出结果.
(1)解:四边形ABCD是垂直四边形;理由如下:
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂直四边形;
(2)证明:设AC、BD交于点E,如图2所示:
∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得:AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+DE2+CE2,
∴AD2+BC2=AB2+CD2;
(3)解:连接CG、BE,如图3所示:
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,![]() ,
,![]() ,∠CAG=∠BAE=90°,
,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,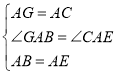 ,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
又∵∠AEC+∠CEB+∠ABE=90°,
∴∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,
∴四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,
∵AC=4,BC=3,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴GE=![]() .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】为了丰富同学们的知识,拓展阅读视野,学习图书馆购买了一些科技、文学、历史等书籍,进行组合搭配成![]() 、
、![]() 、
、![]() 三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
|
|
| |
规格(本/套) | 12 | 9 | 7 |
价格(元/套) | 200 | 150 | 120 |
(1)已知搭配![]() 、
、![]() 两种套型书籍共15套,需购买书籍的花费是2120元,问
两种套型书籍共15套,需购买书籍的花费是2120元,问![]() 、
、![]() 两种套型各多少套?
两种套型各多少套?
(2)若图书馆用来搭配的书籍共有2100本,现将其搭配成![]() 、
、![]() 两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
(3)若图书馆用来搭配的书籍共有122本,现将其搭配成![]() 、
、![]() 、
、![]() 三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.