题目内容
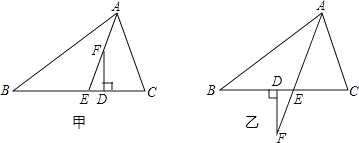
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
【答案】(1) 见解析;(2) 成立,理由见解析.
【解析】试题分析:(1) 根据三角形内角和定理以及角平分线的定义得到∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)=90°﹣
(180°﹣∠B﹣∠C)=90°﹣![]() (∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+
(∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+![]() (∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
试题解析:
解:(1)∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)
(180°﹣∠B﹣∠C)
=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵∠FEC=∠B+∠BAE,
则∠FEC=∠B+90°﹣![]() (∠B+∠C)
(∠B+∠C)
=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥EC,
∴∠EFD=90°﹣∠FEC,
则∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)成立.
证明:同(1)可证:∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠DEF=∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B).
(∠C﹣∠B).

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目