题目内容
 如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,OPn(n为正整数),则点P6的坐标是________;△P5OP6的面积是________.
如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,OPn(n为正整数),则点P6的坐标是________;△P5OP6的面积是________.
(0,-64) 
分析:解题的关键是抓住旋转的三要素:旋转中心原点,旋转方向逆时针,旋转角度.
解答:过P5作P5N⊥轴于N,P5M⊥y轴于M,
∵线段OP0按逆时针方向每次旋转45°,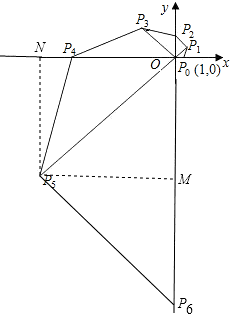
∴旋转6次是45°×6=270°,
∴P6在y轴的负半轴,OP5=25,OP6=26,
由勾股定理得:ON=P5N=16 =P5M,
=P5M,
∴P5(-16 ,-16
,-16 ),P6(0,-64),
),P6(0,-64),
∴△P5OP6的面积是 OP6×P5M=
OP6×P5M= ×64×16
×64×16 =512
=512 .
.
点评:本题将一个图形的旋转放在坐标系中来考查,是一道考查数与形结合的好试题,也为高中后续学习做了良好的铺垫.从考试情况看,还有非常多考生没完全理解旋转的三大要素即中心、方向、角度,故失分的较多.本题综合考查学生旋转和坐标知识.

分析:解题的关键是抓住旋转的三要素:旋转中心原点,旋转方向逆时针,旋转角度.
解答:过P5作P5N⊥轴于N,P5M⊥y轴于M,
∵线段OP0按逆时针方向每次旋转45°,

∴旋转6次是45°×6=270°,
∴P6在y轴的负半轴,OP5=25,OP6=26,
由勾股定理得:ON=P5N=16
 =P5M,
=P5M,∴P5(-16
 ,-16
,-16 ),P6(0,-64),
),P6(0,-64),∴△P5OP6的面积是
 OP6×P5M=
OP6×P5M= ×64×16
×64×16 =512
=512 .
.点评:本题将一个图形的旋转放在坐标系中来考查,是一道考查数与形结合的好试题,也为高中后续学习做了良好的铺垫.从考试情况看,还有非常多考生没完全理解旋转的三大要素即中心、方向、角度,故失分的较多.本题综合考查学生旋转和坐标知识.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

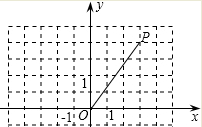 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
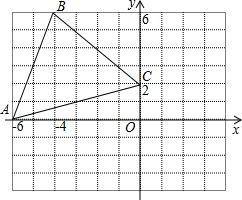 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: