题目内容
已知△ABC中,∠ACB=90゜,AC=BC,过C点任作直线l,过A点、B点分别作l的垂线AM、BN,垂足分别为M、N.若AM=2,BN=4,求MN的长.
解:图1中,MN=6,图2中,MN=2.
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
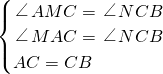 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=NC+CM,
∴MN=AM+BN=2+4=6;
(2)∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
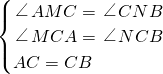 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM=4-2=2.
分析:(1)利用互余关系证明∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,故可证△AMC≌△CNB,从而有AM=CN,MC=BN,利用线段的和差关系证明结论,进而得出答案;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系,进而得出答案.
点评:本题考查了全等三角形的判定与性质.关键是利用互余关系推出对应角相等,证明三角形全等.
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,

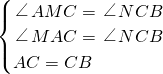 ,
,∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=NC+CM,
∴MN=AM+BN=2+4=6;
(2)∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
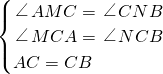 ,
,∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM=4-2=2.
分析:(1)利用互余关系证明∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,故可证△AMC≌△CNB,从而有AM=CN,MC=BN,利用线段的和差关系证明结论,进而得出答案;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系,进而得出答案.
点评:本题考查了全等三角形的判定与性质.关键是利用互余关系推出对应角相等,证明三角形全等.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
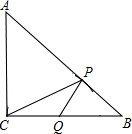 情况;若不可能,请说明理由.
情况;若不可能,请说明理由.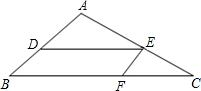 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )