题目内容
【题目】解不等式(组):
(1)10(x﹣3)﹣4≤2(x﹣1)
(2)x﹣![]() ﹣
﹣![]() <1﹣
<1﹣![]()
(3)![]()
(4)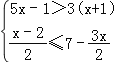 (在数轴上表示解集)
(在数轴上表示解集)
【答案】(1)x≤4;(2)x<3;(3)1<x≤2;(4)2<x≤4
【解析】
试题分析:(1)根据一元一次不等式的解法,去括号,移项,合并同类项,系数化为1即可得解;
(2)根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解;
(3)先求出两个不等式的解集,再求其公共解;
(3)先求出两个不等式的解集,然后在数轴上表示出解集,再找出公共部分即可.
解:(1)去括号得,10x﹣30﹣4≤2x﹣2,
移项得,10x﹣2x≤﹣2+30+4,
合并同类项得,8x≤32,
系数化为1得,x≤4;
(2)去分母得,6x﹣3x﹣(x+8)<6﹣2(x+1),
去括号得,6x﹣3x﹣x﹣8<6﹣2x﹣2,
移项得,6x﹣3x﹣x+2x<6﹣2+8,
合并同类项得,4x<12,
系数化为1得,x<3;
(3)![]() ,
,
解不等式①得,x>1,
解不等式②得,x≤2,
所以,不等式组的解集是1<x≤2;
(4)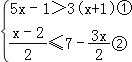 ,
,
解不等式①得,x>2,
解不等式②得,x≤4,
在数轴上表示如下:
![]()
所以,不等式组的解集是2<x≤4.

练习册系列答案
相关题目