Question

【题目】综合与探究

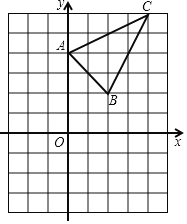
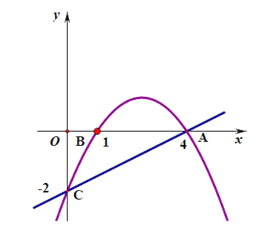
如图，抛物线y=a经过点A、B、C且点C坐标为(0，2)．

（1）求出抛物线的解析式；

（2）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．

（3）点H在线段AC上，若OH最短时，在x轴上找一点N，使△CHN周长最小时，求点N的坐标

（4）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）

（2）D(2,1)

（3）(，0)

（4）存在满足条件的点P，坐标为(0，-2)或(2，1)或(5，-2)或(-3，-14).

【解析】

（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；

（2）可以表示出点D的坐标，过D做DEy轴，交直线AC与点E，表示出DE的长，进一步表示出△DCA的面积，利用二次函数性质，求出点D坐标；

（3）根据垂线段最短确定点H位置，结合相似或三角函数，利用将军饮马模型，确定点N的位置，并求出其坐标；

（4）设出点P的坐标，表示出PM和AM的长，由三角形相似的性质可以得到关于点P的坐标的方程，可求出点P的坐标.

解：（1）由图像得抛物线经过点A(4,0)、B(1,0)、C (0，2)，把A、B、C三点坐标代入解析式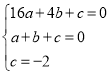得：，解得，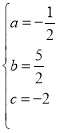

∴抛物线解析式为：

（2）∵D在直线AC上方的抛物线上，

∴设D坐标为()（0＜t＜4），

如图，过D作DEy轴，交直线AC与点E，

则点E坐标为()，

∴

∴

∵-1＜0，

∴当t=2时，S△DCA有最大值4，此时D坐标为(2,1);

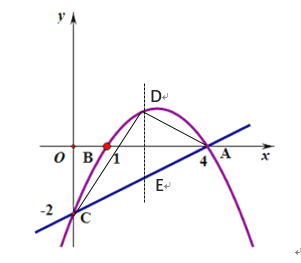
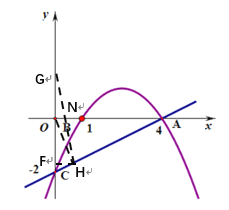
（3）如图，∵H在AC上，且OH最短，

∴OH为点O到AC的垂线段.

作OH⊥AC垂足为H，作OH⊥y轴，设点C关于x轴的对称点为G，连接HG，交x轴与点N，此时，△CHN周长最小.

∵△CHF∽△CAO，

∴

∵△CHF∽△CHO，

∴

∴

∴，，

∵点G与点C关于x轴对称，

∴OG=2

∵△GON∽△GFH，

∴

即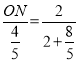：，解得ON=

∴点N坐标为(，0);

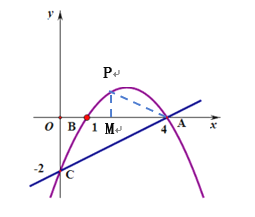
（4）如图，设点P的坐标为()，则M坐标为()，

∴，

∵A(4,0)、C (0，2)，

∴OA=4，OC=2

∵PM⊥x轴，

∴∠PMA=∠COA=90°

∴当△PAM和△CAO相似时，有两种情况.

①当时，，

解得：m=4或m=2,或m=0，

当m=4时，点P在x轴上，不合题意，舍去，

当m=0时，点P(0，-2)，

当m=2是，点P(2，1)；

②当时，，

解得：m=4或m=5,或m=-3，

当m=5时，点P(5，-2)，

当m=-3时，点P(-3，-14)，

综上所述：存在满足条件的点P，其坐标为(0，-2)或(2，1)或(5，-2)或(-3，-14).