Question

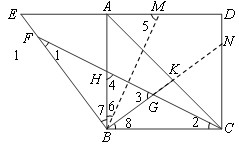
如图，AC为正方ABCD形的一条对角线，点E为DA边延长线上的一点，连接BE，在BE上取一点F，使BF=BC，过点B作BK⊥BE于B，交AC于点K，连接CF，交AB于点H，交BK于点G。

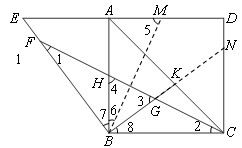
（1）求证：BH=BG；
（2）求证：BE=BG+AE。

Answer 1

解：（1）在正方形ABCD中，∠ABC=90° 又∵ ∴ ∴ 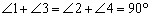∵ ∴ ∴ ∴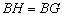。 （2）延长BG交CD于N 在正方形ABCD中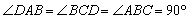， ∴∠EAB=∠BCD=90° 又∵∠FBK=90° ∴ ∴ 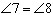∴ 又∵AB∥CN ∴△EAB∽△NCB ∴。