题目内容
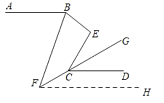
【题目】如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝36°，则∠E＝（ ）
A.82°B.84°C.97°D.90°
【答案】B
【解析】
过F作FH∥AB，依据平行线的性质，可设∠ABF＝∠EBF＝
＝∠BFH，∠DCG＝∠ECG＝β＝∠CFH，根据四边形内角和以及∠E∠F＝36°，即可得到∠E的度数．
如图，过F作FH∥AB，
∵AB∥CD，
∴FH∥AB∥CD，
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，
∴可设∠ABF＝∠EBF＝＝∠BFH，∠DCG＝∠ECG＝β＝∠CFH，
∴∠ECF＝180°β，∠BFC＝∠BFH∠CFH＝β，
∴四边形BFCE中，∠E＋∠BFC＝360°α（180°β）＝180°（β）＝180°∠BFC，
即∠E＋2∠BFC＝180°，①
又∵∠E∠BFC＝36°，
∴∠BFC＝∠E36°，②
∴由①②可得，∠E＋2（∠E36°）＝180°，
解得∠E＝84°，
故选：B．
练习册系列答案
相关题目
