题目内容
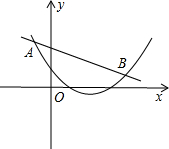
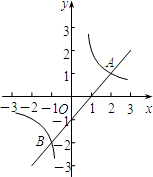 如图,直线y=x+m与双曲线
如图,直线y=x+m与双曲线 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)求出点B的坐标;
(3)直接写出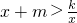 时x的取值范围.
时x的取值范围.
解:(1)∵把A(2,1)代入y=x+m得:1=2+m,
∴m=-1,
∵把A(2,1)代入y= 得:1=
得:1=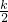 ,
,
∴k=2;
(2)∵解由y=x-1和y= 组成的方程组
组成的方程组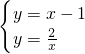 得:
得: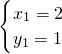 ,
,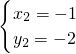 ,
,
又∵A(2,1),
∴B的坐标是(-1,-2);
(3)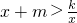 时x的取值范围是-1<x<0或x>2.
时x的取值范围是-1<x<0或x>2.
分析:(1)把A的坐标分别代入两函数的解析式即可求出答案;
(2)解由两函数组成的方程组,求出方程组的解,即可得出答案;
(3)结合图象和两交点的横坐标即可得出答案.
点评:本题考查了用待定系数法求出反比例函数和一次函数的解析式,求两函数的交点坐标,函数的图象等知识点,主要考查学生的计算能力,题目比较典型,是一道比较好的题目.
∴m=-1,
∵把A(2,1)代入y=
 得:1=
得:1=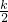 ,
,∴k=2;
(2)∵解由y=x-1和y=
 组成的方程组
组成的方程组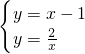 得:
得: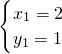 ,
,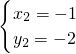 ,
,又∵A(2,1),
∴B的坐标是(-1,-2);
(3)
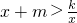 时x的取值范围是-1<x<0或x>2.
时x的取值范围是-1<x<0或x>2.分析:(1)把A的坐标分别代入两函数的解析式即可求出答案;
(2)解由两函数组成的方程组,求出方程组的解,即可得出答案;
(3)结合图象和两交点的横坐标即可得出答案.
点评:本题考查了用待定系数法求出反比例函数和一次函数的解析式,求两函数的交点坐标,函数的图象等知识点,主要考查学生的计算能力,题目比较典型,是一道比较好的题目.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
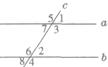 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )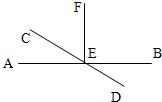 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )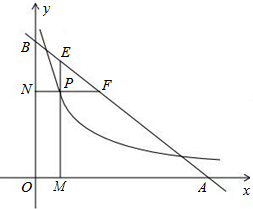 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数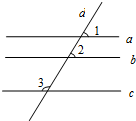 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).