题目内容
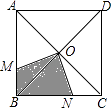
【题目】如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( ) 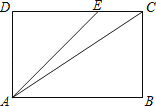
A.q<r,QE=RC
B.q<r,QE<RC
C.q=r,QE=RC
D.q=r,QE<RC
【答案】D
【解析】解:∵在矩形ABCD中,AB∥CD,
∵AP:PD=4:1,AQ:QE=4:1,
∴ ![]() ,
,
∴PQ∥CD,
∴ ![]() =4,
=4,
∵平行线间的距离相等,
∴q=r,
∵ ![]() =4,∴
=4,∴ ![]() =
= ![]() ,
,
∵AE<AC,
∴QE<CR.
故选D.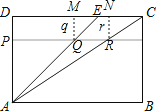
根据矩形的性质得到AB∥CD,根据已知条件得到 ![]() ,根据平行线分线段成比例定理得到PQ∥CD,
,根据平行线分线段成比例定理得到PQ∥CD, ![]() =4,根据平行线间的距离相等,得到q=r,证得
=4,根据平行线间的距离相等,得到q=r,证得 ![]() =
= ![]() ,于是得到结论.本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.
,于是得到结论.本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目