题目内容
 28、如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.
28、如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG,如果存在点P,能使得S△ABC=S△ABG,求∠C的取值范围.
分析:(1)证得△ACP≌△BCP即可;
(2)加上(1)的结论,证得△ACE≌△BCF即可;
(3)假设存在点P,能使得S△ABC=S△ABG,由(2)得到的AE=BF,则新三角形ABG也为等腰三角形,根据底边都为AB,面积相等,得到高相等,所以AC=AE,即三角形ACE为等腰三角形,则底角∠C为锐角,即可得到∠C的取值范围.
(2)加上(1)的结论,证得△ACE≌△BCF即可;
(3)假设存在点P,能使得S△ABC=S△ABG,由(2)得到的AE=BF,则新三角形ABG也为等腰三角形,根据底边都为AB,面积相等,得到高相等,所以AC=AE,即三角形ACE为等腰三角形,则底角∠C为锐角,即可得到∠C的取值范围.
解答:证明:(1)∵△ABC是等腰三角形,CH是底边上的高线,
∴AC=BC,∠ACP=∠BCP.
又∵CP=CP,
∴△ACP≌△BCP.
∴∠CAP=∠CBP,即∠CAE=∠CBF.
(2)∵∠ACE=∠BCF,∠CAE=∠CBF,AC=BC,
∴△ACE≌△BCF.
∴AE=BF.
(3)解:由(2)知△ABG是以AB为底边的等腰三角形,
∴S△ABC=S△ABG.
∴AE=AC.
①当∠C为直角或钝角时,在△ACE中,不论点P在CH何处,均有AE>AC,所以结论不成立;
②当∠C为锐角时,∠A=90°-1/2∠C,而∠CAE<∠A,要使AE=AC,只需使∠C=∠CEA,
此时,∠CAE=180°-2∠C,
只须180°-2∠C<90°-1/2∠C,解得60°<∠C<90°.

∴AC=BC,∠ACP=∠BCP.
又∵CP=CP,
∴△ACP≌△BCP.
∴∠CAP=∠CBP,即∠CAE=∠CBF.
(2)∵∠ACE=∠BCF,∠CAE=∠CBF,AC=BC,
∴△ACE≌△BCF.
∴AE=BF.
(3)解:由(2)知△ABG是以AB为底边的等腰三角形,
∴S△ABC=S△ABG.
∴AE=AC.
①当∠C为直角或钝角时,在△ACE中,不论点P在CH何处,均有AE>AC,所以结论不成立;
②当∠C为锐角时,∠A=90°-1/2∠C,而∠CAE<∠A,要使AE=AC,只需使∠C=∠CEA,
此时,∠CAE=180°-2∠C,
只须180°-2∠C<90°-1/2∠C,解得60°<∠C<90°.

点评:本题考查了全等三角形的判定与性质及等腰三角形的性质;两条线段在不同的三角形中要证明相等时,通常是利用全等来进行证明.需注意已证得条件在以后证明中的应用,以及分情况进行讨论等情况.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
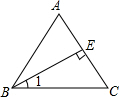 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
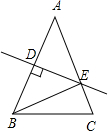 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=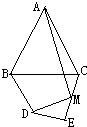 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.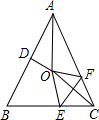 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是