题目内容
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′=θ, ,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .
,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .



 ,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .
,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .


2
试题分析:先根据三角形的内角和定理求得∠DE′E=30°,再根据含30°的直角三角形的性质求解即可.
∵∠DEE'=90°,∠EDE′=60°,
∴∠DE′E=30°,
∴n=2.
点评:解题的关键是熟练掌握旋转对应边的夹角是旋转角,注意数形结合思想思想的应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

 ,则CC′= cm.
,则CC′= cm.

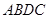 中,
中, 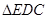 是由
是由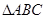 绕顶点
绕顶点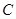 旋转
旋转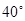 所得, 顶点
所得, 顶点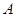 恰好转到
恰好转到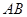 上一点
上一点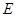 的位置, 则
的位置, 则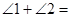 ( )
( ) 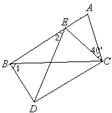

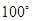
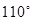




 绕点
绕点 逆时针旋转30°到正方形
逆时针旋转30°到正方形 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )



