题目内容
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=![]() ,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )
,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
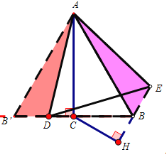
在CB的反向延长线上取一点B’,使得BC=B’C,连接AB’,易证△AB’D≌△ABE,可得∠ABE=∠B’=60°,因此点E的轨迹是一条直线,过点C作CH⊥BE,则点H即为使得BE最小时的E点的位置,然后根据直角三角形的性质和勾股定理即可得出答案.
解:在CB的反向延长线上取一点B’,使得BC=B’C,连接AB’,
∵∠ACB=90°,∠ABC=60°,
∴△AB’B是等边三角形,
∴∠B’=∠B’AB=60°,AB’=AB,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠B’AD+∠DAB=∠DAB+∠BAE,
∴∠B’AD=∠BAE,
∴△AB’D≌△ABE(SAS),
∴∠ABE=∠B’=60°,
∴点E在直线BE上运动,
过点C作CH⊥BE于点H,则点H即为使得BE最小时的E点的位置,
∠CBH=180°-∠ABC-∠ABE=60°,
∴∠BCH=30°,
∴BH=![]() BC=
BC=![]() ,
,
∴CH=![]() =
=![]() .
.
即BE的最小值是![]() .
.
故选C.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目