题目内容

(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
4.
(1)求证:AB=AD;
(2)求△BCD的面积.
分析:(1)根据两直线平行,内错角相等可得∠1=∠2,再根据角平分线的定义可得∠2=∠3,然后求出∠1=∠3,再根据等角对等边即可得证;
(2)过点D作DE⊥BC于E,根据∠A=120°求出∠2=30°,然后在Rt△BDE中解直角三角形求出DE、DE的长度,在Rt△CDE中,解直角三角形求出CD的长,即可得到AD的长,然后根据等腰梯形的性质求出BC的长,然后利用三角形的面积公式列式计算即可得解.
解答: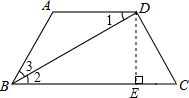
(1)证明:∵AD∥BC,
∴∠1=∠2,
又∵BD平分∠ABC,
∴∠2=∠3,
∴∠1=∠3,
∴AB=AD;
(2)解:过点D作DE⊥BC于E,
∵∠A=120°,
∴∠ABC=180°-∠A=180°-120°=60°,
∴∠2=∠3=
(180°-120°)=30°,
在Rt△BDE中,DE=
BD=2
,BE=
BD=
×4
=6,
∵四边形ABCD是等腰梯形,
∴∠C=∠ABC=60°,
在Rt△CDE中,CD=DE÷sin60°=2
÷
=4,
∴AD=AB=CD=4,
∴BC=2(BE-AD)+AD=2(6-4)+4=8,
∴△BCD的面积=
BC•DE=
×8×2
=8
.
点评:本题考查了等腰梯形的性质,角平分线的定义,以及解直角三角形,(2)中作辅助线构造出直角三角形然后求出边BC的长度是解题的关键.
练习册系列答案
相关题目
 (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4 (1)证明:∵AD∥BC,
(1)证明:∵AD∥BC, (1)证明:∵AD∥BC,
(1)证明:∵AD∥BC,
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2007•昌平区二模)如图,△ABC中,DE∥BC 若
(2007•昌平区二模)如图,△ABC中,DE∥BC 若 (2007•昌平区二模)如图:六边形ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD⊥BD.已知FD=4cm,BD=3cm.则六边形ABCDEF的面积是
(2007•昌平区二模)如图:六边形ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD⊥BD.已知FD=4cm,BD=3cm.则六边形ABCDEF的面积是