题目内容
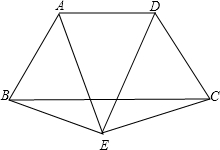已知：如图，等腰梯形ABCD中，AB=CD，AD∥BC，E是梯形外一点，且EA=ED，求证：EB=EC．
分析：由等腰梯形的性质知，AB=CD，∠BAD=∠CDA，由等边对等角得到∠EAD=∠EDA证得∠EAB=∠EDC，再由SAS证得△ABE≌△DCE?EB=EC
解答：证明：在等腰梯形ABCD中AB=CD，∴∠BAD=∠CDA．
∵EA=ED，
∴∠EAD=∠EDA．
∴∠EAB=∠EDC．（2分）
在△ABE和△DCE中
∵
，
∴△ABE≌△DCE．（5分）
∴EB=EC．（6分）
∵EA=ED，
∴∠EAD=∠EDA．
∴∠EAB=∠EDC．（2分）
在△ABE和△DCE中
∵
|
∴△ABE≌△DCE．（5分）
∴EB=EC．（6分）
点评：本题主要考查了等腰梯形的性质及全等三角形的判定的理解及运用．
练习册系列答案
相关题目
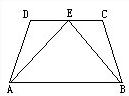20、已知：如图，等腰梯形ABCD中，AB∥DC，E为DC的中点，求证：∠EAB=∠EBA．
（2007•昌平区二模）已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC，∠A=120°，BD=
已知，如图，等腰梯形ABCD中，AB∥CD，对角线AC⊥BD于O，BC=13