题目内容
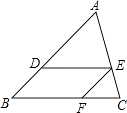
【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

【答案】(1)2;(2)5;(3)见解析.
【解析】
(1)根据CD⊥AB即可进行判断;
(2)利用勾股定理求解即可;
(3)根据勾股定理可得BD2=BC2﹣CD2,AD2=AC2﹣CD2,再利用完全平方公式(AD+BD)2=AD2+2AD·BD+BD2,代入整理,根据勾股定理的逆定理即可得证.
(1)∵CD⊥AB,
∴△ACD与△BCD都是直角三角形,
故图中有2个直角三角形;
(2)在Rt△ACD中,
CD=![]() =5;
=5;
(3)在Rt△ACD中,AD2=AC2﹣CD2,
在Rt△BCD中,BD2=BC2﹣CD2,
∵CD2=AD·DB,
∴(AD+BD)2=AD2+2AD·BD+BD2
= AC2﹣CD2+2 CD2+BC2﹣CD2
= AC2+ BC2=AB2,
则△ABC是直角三角形.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.