Question

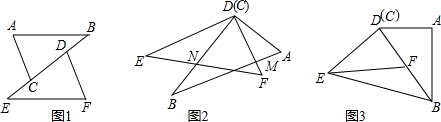
如图1所示，已知在△ABC和△DEF中，∠A=∠F=90°，∠B=∠E，EC=BD．
（1）试说明：△ABC≌△FED的理由；
（2）若图形经过平移和旋转后得到如图2，若∠ADF=30°，∠E=37°，试求∠DHB的度数；
（3）若将△ABC继续绕点D旋转后得到图3，此时D、B、F三点在同一条直线上，若DF：FB=3：2，连接EB，已知△ABD的周长是12，且AB-AD=1，你能求出四边形ABED的面积吗？若能，请求出来；若不能，请说明理由．

Answer 1

分析：（1）求出BC=DE，根据AAS推出△ABC≌△FED即可；
（2）根据全等三角形的性质得出∠ADB=∠FDE=53°，∠B=∠E=37°，求出∠ADH=23°代入∠DHB=∠A+∠ADH求出即可；
（3）设AD的长为x，AB的长为y，则BD=

5

3

x，根据题意得出方程组

x+ 5 3 x+y=12 y-x=1

，求出x、y的值，得出AD=3，AB=4，BD=5，根据全等三角形性质得出EF=AB=4，根据三角形的面积公式求出△BDE和△ABD的面积即可．

解答：解：（1）理由是：∵BD=EC，
∴BD+CD=EC+CD，
∴BC=DE，
在△ABC和△FED中

∠A=∠F ∠B=∠E BC=DE

∴△ABC≌△FED（AAS）；

（2）∵△ABC≌△FED，
∴∠ADB=∠FDE=90°-37°=53°，∠B=∠E=37°，
∴∠ADH=53°-30°=23°
∴∠DHB=∠A+∠ADH=90°+23°=113°；

（3）设AD的长为x，AB的长为y，则BD=

5

3

x，
根据题意得：

x+ 5 3 x+y=12 y-x=1

，
解得：x=3，y=4，
即AD=3，AB=4，BD=5，
由（1）得：△ABD≌△FED，
∴EF=AB=4，
∴S_{四边形ABED}=S_△BDE+S_△ABD=

1

2

×5×4+

1

2

×3×4=16．

点评：本题考查了全等三角形的性质和判定，三角形的面积，解方程组等知识点的综合运用．