题目内容
如图1所示,已知在△ABD和△AEC中,AC=AD,∠CAD=∠BAE,AB=AE
(1)如图1,试说明:△ABD≌△AEC;
(2)如图1,若∠CAD=35°,∠E=56°,∠D=40°,
①试求:∠EOB的度数;
②将△AEC绕点A逆时针旋转α度(0°<α<180°),问当α为多少度时,直线CE分别与△ABD的三边所在的直线垂直?(请直接写出答案).
(3)如图2将△AEC绕点A顺时针旋转后得到△ABD,并使点D,E,A三点在同一条直线上,若AD=2AB,连接CD,若△CDE的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由.
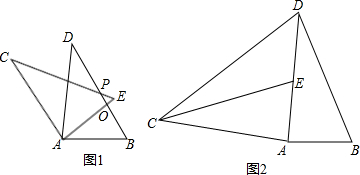
(1)如图1,试说明:△ABD≌△AEC;
(2)如图1,若∠CAD=35°,∠E=56°,∠D=40°,
①试求:∠EOB的度数;
②将△AEC绕点A逆时针旋转α度(0°<α<180°),问当α为多少度时,直线CE分别与△ABD的三边所在的直线垂直?(请直接写出答案).
(3)如图2将△AEC绕点A顺时针旋转后得到△ABD,并使点D,E,A三点在同一条直线上,若AD=2AB,连接CD,若△CDE的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由.

分析:(1)首先证明∠CAE=∠DAB,再加上条件AC=AD,AB=AE可利用SAS定理证明△ABD≌△AEC;
(2)①计算出∠BAE和∠B的度数,再利用三角形的外角与内角的关系可得∠EOB的度数;
②要分三种情况进行讨论C′E′⊥AD时;CE′⊥BD时;C′E′⊥AB时;
(3)首先证明点E为AD中点,再根据△CDE的面积为6cm2,可得△CAE的面积也为6cm2,△ABD的面积为6cm2,可得四边形ABDC的面积.
(2)①计算出∠BAE和∠B的度数,再利用三角形的外角与内角的关系可得∠EOB的度数;
②要分三种情况进行讨论C′E′⊥AD时;CE′⊥BD时;C′E′⊥AB时;
(3)首先证明点E为AD中点,再根据△CDE的面积为6cm2,可得△CAE的面积也为6cm2,△ABD的面积为6cm2,可得四边形ABDC的面积.
解答:(1)证明:∵∠CAD=∠BAE,
∴∠CAD+∠DAE=∠BAE+∠DAE,
即∠CAE=∠DAB,
在△ABD和△AEC中
,
∴△ABD≌△AEC(SAS);
(2)解:①由(1)知△ABD≌△AEC,
∴∠B=∠E=56°,
∵∠CAD=35°,
∴∠BAE=∠CAD=35° ,
,
∴∠EOB=∠BAE+∠B=35°+56°=91°;
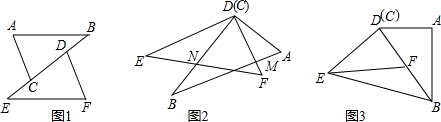
②当C′E′⊥AD时,如图3,
∵∠D=40°,∠B=56°,
∴∠DAB=180°-40°-56°=84°,
∵∠E=56°,
∴∠DAE′=180°-56°-90°=34°,
∴∠E′AB=84°-34°=50°,
∴α=∠E′AE=50°-35°=15°;
当CE′⊥BD时,如图4,延长C′E′交DB于点F,
则∠E′FB=90°,
∵∠E′=∠E=56°,
∴∠FE′A=124°,
∵∠B=56°,
∴∠E′AB=360°-90°-124°-56°=90°,
∴α=∠E′AB-∠EAB=90°-35°=55°;
α=55°,
当C′E′⊥AB时,如图5,
∵∠E′=∠E=56°,
∴∠E′AF=180°-90°-56°=34°,
∵∠EAB=35°,
∴∠EAE′=α=180°-34°-35°=111°;
(3)解:能求出四边形ABDC的面积.
∵△ABD是由△AEC绕点A逆时针旋转而得,
∴△ABD≌△AEC,
∴AB=AE,
∵AD=2AB,
∴AD=2AE,即点E为AD中点.
∵△CDE的面积为6cm2,
∴△CAE的面积也为6cm2,△ABD的面积为6cm2,
∴四边形ABDC的面积为18cm2.
∴∠CAD+∠DAE=∠BAE+∠DAE,
即∠CAE=∠DAB,
在△ABD和△AEC中
|
∴△ABD≌△AEC(SAS);
(2)解:①由(1)知△ABD≌△AEC,
∴∠B=∠E=56°,
∵∠CAD=35°,
∴∠BAE=∠CAD=35°
 ,
,∴∠EOB=∠BAE+∠B=35°+56°=91°;
②当C′E′⊥AD时,如图3,
∵∠D=40°,∠B=56°,
∴∠DAB=180°-40°-56°=84°,
∵∠E=56°,

∴∠DAE′=180°-56°-90°=34°,
∴∠E′AB=84°-34°=50°,
∴α=∠E′AE=50°-35°=15°;
当CE′⊥BD时,如图4,延长C′E′交DB于点F,
则∠E′FB=90°,
∵∠E′=∠E=56°,
∴∠FE′A=124°,

∵∠B=56°,
∴∠E′AB=360°-90°-124°-56°=90°,
∴α=∠E′AB-∠EAB=90°-35°=55°;
α=55°,
当C′E′⊥AB时,如图5,
∵∠E′=∠E=56°,
∴∠E′AF=180°-90°-56°=34°,
∵∠EAB=35°,
∴∠EAE′=α=180°-34°-35°=111°;
(3)解:能求出四边形ABDC的面积.
∵△ABD是由△AEC绕点A逆时针旋转而得,
∴△ABD≌△AEC,
∴AB=AE,
∵AD=2AB,
∴AD=2AE,即点E为AD中点.
∵△CDE的面积为6cm2,
∴△CAE的面积也为6cm2,△ABD的面积为6cm2,
∴四边形ABDC的面积为18cm2.
点评:本题考查了全等三角形的判定与性质以及图形的旋转,判定两三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”,需要熟练掌握.

练习册系列答案
相关题目

 ,
, ,
,
 ≌
≌ ;
;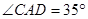 ,
, ,
, ,
, 的度数
的度数 度(
度( ),问当
),问当 ,连接CD,若
,连接CD,若 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
 ,
, ,
,
 ≌
≌ ;
; ,
, ,
, ,
, 的度数
的度数 度(
度( ),问当
),问当 ,连接CD,若
,连接CD,若 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。