题目内容
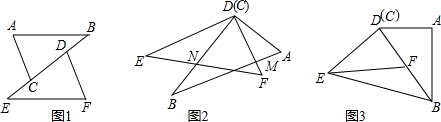
如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.

分析:(1)由EC=BD,等式左右两边都加上DC,得到ED=BC,再由∠B=∠E,AB=EF,利用SAS可证明三角形ABC与三角形FED全等;
(2)由三角形ABC与三角形FED全等,根据全等三角形的对应角相等,得到∠EDF=∠BDA,等号两边都减去∠BDF,得到∠EDB=∠ADF,由∠EDB的度数得到∠ADF的度数,在三角形AMD中,由∠ADF及∠A的度数,利用三角形的内角和定理即可求出∠AMD的度数;
(3)由BD=2DF,得到为DB的中点,可得DF=BF,利用等底同高可得三角形DEF与三角形EFB面积相等,又三角形ABD与三角形DEF全等,得到三角形ABD与三角形DEF面积相等,可得三角形DEF,三角形EFB与三角形ABD的面积都相等,由三角形EFB的面积可得出其它两三角形的面积,三者相加可得出四边形ABED的面积.
(2)由三角形ABC与三角形FED全等,根据全等三角形的对应角相等,得到∠EDF=∠BDA,等号两边都减去∠BDF,得到∠EDB=∠ADF,由∠EDB的度数得到∠ADF的度数,在三角形AMD中,由∠ADF及∠A的度数,利用三角形的内角和定理即可求出∠AMD的度数;
(3)由BD=2DF,得到为DB的中点,可得DF=BF,利用等底同高可得三角形DEF与三角形EFB面积相等,又三角形ABD与三角形DEF全等,得到三角形ABD与三角形DEF面积相等,可得三角形DEF,三角形EFB与三角形ABD的面积都相等,由三角形EFB的面积可得出其它两三角形的面积,三者相加可得出四边形ABED的面积.
解答:解:(1)∵EC=BD(已知),
∴EC+CD=BD+DC,即ED=BC,
在△ABC和△FED中,
,
∴△ABC≌△FED(SAS);
(2)∵△ABC≌△FED,
∴∠EDF=∠BDA,
∴∠EDF-∠BDF=∠BDA-∠BDF,又∠EDB=25°,
∴∠EDB=∠ADF=25°,又∠A=66°,
∴∠AMD=180°-66°-25°=89°;
(3)能求出四边形ABED的面积,方法为:
∵△ABC≌△FED,
∴S△ABC=S△FED,
∵DB=2DF,即F为BD中点,
∴DF=BF,又S△EFB=5,
∴S△EDF=S△EFB=S△ABC=5,
∴SABCD=S△EDF+S△EFB+S△ABC=15.
∴EC+CD=BD+DC,即ED=BC,
在△ABC和△FED中,
|
∴△ABC≌△FED(SAS);
(2)∵△ABC≌△FED,
∴∠EDF=∠BDA,
∴∠EDF-∠BDF=∠BDA-∠BDF,又∠EDB=25°,
∴∠EDB=∠ADF=25°,又∠A=66°,
∴∠AMD=180°-66°-25°=89°;
(3)能求出四边形ABED的面积,方法为:
∵△ABC≌△FED,
∴S△ABC=S△FED,
∵DB=2DF,即F为BD中点,
∴DF=BF,又S△EFB=5,
∴S△EDF=S△EFB=S△ABC=5,
∴SABCD=S△EDF+S△EFB+S△ABC=15.
点评:此题考查了全等三角形的判定与性质,平移及旋转的性质,利用了等量代换及转化的思想,第三问的关键是根据题意得出F为BD的中点,进而利用等底同高得到三角形面积相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

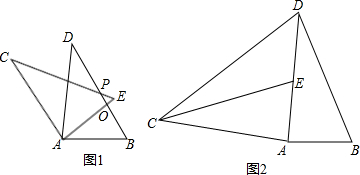
 ,
, ,
,
 ≌
≌ ;
; ,
, ,
, ,
, 的度数
的度数 度(
度( ),问当
),问当 ,连接CD,若
,连接CD,若 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
 ,
, ,
,
 ≌
≌ ;
; ,
, ,
, ,
, 的度数
的度数 度(
度( ),问当
),问当 ,连接CD,若
,连接CD,若 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。