题目内容
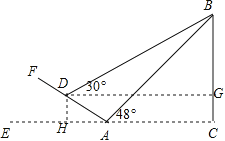
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

【答案】13米.
【解析】试题分析:根据矩形性质得出DG=CH,CG=DH,再利用锐角三角函数的性质求出问题即可.
试题解析:如图,过点D作DG⊥BC于GDH⊥CE于H,
则四边形DHCG为矩形.
故DG=CH,CG=DH,
在直角三角形AHD中,
∵∠DAH=30°,AD=6,
∴DH=3,AH=3![]() ,
,
∴CG=3,
设BC为x,
在直角三角形ABC中,AC=![]() ,
,
∴DG=3![]() +
+![]() ,BG=x-3,
,BG=x-3,
在直角三角形BDG中,∵BG=DGtan30°,
∴x-3=(3![]() +
+![]() )
)![]()
解得:x≈13,
∴大树的高度为:13米.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】如图所示的日历中,任意圈出一竖列相邻的三个数,设中间一个数为a,则这三个数之和为(用含a的式子表示)
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |