题目内容
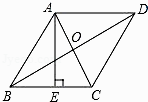
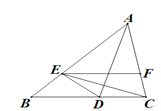
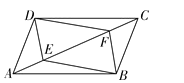
【题目】如图，点 E，F 是ABCD 对角线上两点，在条件①DE＝BF；②∠ADE＝∠CBF； ③AF＝CE；④∠AEB＝∠CFD 中，添加一个条件，使四边形 DEBF 是平行四边形，可添加 的条件是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】D
【解析】分别添加条件①②③④，根据平行四边形的判定方法判定即可．
添加条件①，不能得到四边形DEBF是平行四边形，故①错误；
添加条件②∠ADE＝∠CBF．∵ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠DAC=∠BCA，∴△ADE≌△CBF，∴DE=BF，∠DEA=∠BFC，∴∠DEF=∠BFE，∴DE ∥BF，∴DEBF是平行四边形，故②正确；
添加条件③AF＝CE．易得AD=BC，∠DAC=∠BCA，∴△ADF≌△CBE，∴DF=BE，∠DFE=∠BEF，∴DF ∥BE，∴DEBF是平行四边形，故③正确；
添加条件④∠AEB＝∠CFD．∵ABCD是平行四边形，DC=AB，DC∥AB，∴∠DCF=∠BAE．∵∠AEB＝∠CFD，∴△ABE≌△CDF，∴DF=BE．∵∠AEB＝∠CFD，∴∠DFE=∠BEF，∴DF ∥BE，∴DEBF是平行四边形，故④正确．
综上所述：可添加的条件是：②③④．
故选D．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
